MA2051 - Ordinary Differential Equations
Sample Exam #2 - A96

Originally Given 1995 D Term 





TEST I




Covers 1.1-1.2, 2.1-2.2, 3.1-3.3.2, 3.5-3.8, 4.1-4.2.1, 5.1-5.3.


Instructions: Do your work on the paper provided.  Put 
your name, section number and PLA's name on that paper.  Work 
neatly.  Show your work. 


JUSTIFY YOUR ANSWERS.





1 (70 pts) 

  A radioactive 
isotope decays at a rate proportional to its mass.  The isotope is 
being bombarded by a neutron beam that creates new isotope at a constant 
rate.  A model for the mass y of isotope at time t is

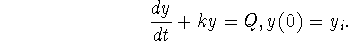
 displaymath40 



    

	A)
    
 Explain the meaning of the terms k y and Q appearing in 
    the differential equation.  Determine whether these terms act to 
    increase or decrease the mass of isotope.


    

	B)
    
 Sketch graphs of the solution of this initial-value problem 
    for a variety of initial values.


    

	C)
    
 Find the steady state(s) of y, if any.


    

	D)
    
 Find a particular solution of this differential equation.


    

	E)
    
 Find a general solution of this differential equation.


    

	F)
    
 Find a solution of the initial-value problem.


    

	G)
    
 Determine the stability of any steady state(s).





2 (20 pts) 

  A simple model for 
the population of the U.S. in the 1970's and 1980's is P' = 0.01 P, 
P(1970) = 205.  Use one step of Euler's method to estimate the year
the population would double.





3 (10 pts) 

 Find a particular 
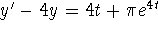solution of  tex2html_wrap_inline56 .


 






  

    

© 1996 by Will Brother.
All rights Reserved. File last modified on September 16, 1996.