MA2051 - Ordinary Differential Equations
Solutions to Sample Exam #2 - A96
Originally Given 1995 D Term
-
1
-
-
A,B,C)
y' = -ky + Q; -k y is decay (decreasing y because of
negative sign) proportional to mass, and Q is constant rate of
increase (assuming Q > 0).
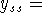 constant forces
constant forces 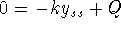 and
and 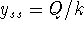 .
.
-
D)
-
Use
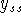 as a particular solution or apply undetermined
coefficients to this linear, constant coefficient equation to
obtain
as a particular solution or apply undetermined
coefficients to this linear, constant coefficient equation to
obtain 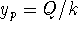 .
.
-
E)
-
Solve y' + ky = 0 for
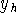 via characteristic equations to
obtain
via characteristic equations to
obtain 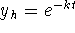 . Use
. Use 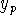 from above to write
from above to write 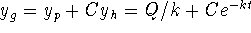 .
.
-
F)
- Use
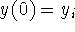 in
in 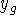 to find C:
to find C: 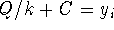 yields
yields
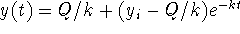 .
.
-
G)
-
The steady state
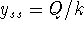 is stable; see the graph
above or use the solution in the previous part to argue
is stable; see the graph
above or use the solution in the previous part to argue 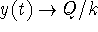 for all
for all 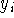 .
.
-
2
-
- Apply Euler with unknown step size ,
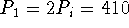 :
:
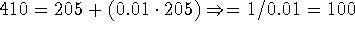 .
Hence, the population of the U.S. will double from 205 million to 410
million in about the year 1970 + 100 = 2070.
.
Hence, the population of the U.S. will double from 205 million to 410
million in about the year 1970 + 100 = 2070.
- (Same as 3.8/6 with y replacing u, t replacing x.) Apply
undetermined coefficients for a polynomial (4t) and an exponential
(
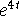 ) forcing term; first guess is
) forcing term; first guess is 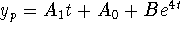 .
But a solution of the homogeneous equation y' - 4y = 0 is
.
But a solution of the homogeneous equation y' - 4y = 0 is 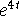 .
Hence, the final form should be
.
Hence, the final form should be
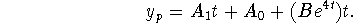
-
3
-
Substitution yields
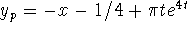 .
.
© 1996 by Will Brother.
All rights Reserved. File last modified on September 16, 1996.
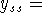 constant forces
constant forces 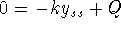 and
and 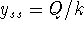 .
.
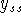 as a particular solution or apply undetermined
coefficients to this linear, constant coefficient equation to
obtain
as a particular solution or apply undetermined
coefficients to this linear, constant coefficient equation to
obtain 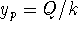 .
.
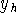 via characteristic equations to
obtain
via characteristic equations to
obtain 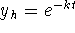 . Use
. Use 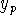 from above to write
from above to write 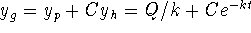 .
.
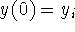 in
in 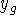 to find C:
to find C: 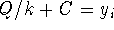 yields
yields
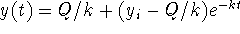 .
.
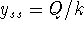 is stable; see the graph
above or use the solution in the previous part to argue
is stable; see the graph
above or use the solution in the previous part to argue 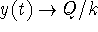 for all
for all 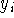 .
.