MA2051--C97: TEST II

1. (30 points) Work with the following differential equation:

$$2 y^{\prime\prime}- y^{\prime}- 3y = 9 e^{-3t}$$

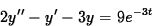
(a)

Find two linearly independent solutions for the corresponding homogeneous equation. Prove that your solutions really are linearly independent.

(b)

Find a particular solution for the differential equation.

(c)

Find the solution that satisfies the initial conditions y(0) = 1/2, $y^{\prime}(0) = 3/2$.

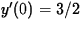(d)

Describe the behavior of the general solution for large values of t. What part of the solution is transient? Is there a limiting periodic solution?

2. (30 points) A 6 kg mass is suspended from a spring that extended 2 cm when the weight was attached. Assume that friction damping can be ignored. You pull the mass down 3 cm (more) and release it from rest.

(a)

Write down the mathematical model for this system. Use the given data to specify the numerical values for the parameters in the model. (Be careful with units.)

(b)

Solve the initial value problem derived in part (a).

(c)

What is the amplitude of the motion? How long does it take for the mass to travel from its highest position to its lowest position?

(d)

What is the velocity of the mass when it passes through the equilibrium position (x=0)?

3. (30 points) Consider the following initial value problem

$$y^{\prime}(t) = 5y(t) - 3z(t), \rule{3ex}{0pt} y(0) = 50 ,$$

$$z^{\prime}(t) = 9y(t) - 7z(t), \rule{3ex}{0pt} z(0) = 50 .$$

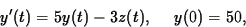
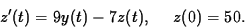
(a)

Give the characteristic equation and find its roots. Use the roots to find two linearly independent solution pairs and use them to give the general solution for the system.

(b)

Find the solution satisfying the given initial conditions.

(c)

Is it possible to find initial conditions (different than the given initial conditions) so that the solution curve converges to the origin (y,z) = (0,0) as t goes to infinity?

4. (10 points) Choose p so that the following spring-mass model is critically damped:

$$x^{\prime\prime}+ p x^{\prime}+ 4 x = 0,\quad x(0) = x_i,\; x^{\prime}(0) = v_i.$$

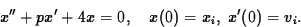
Show that the solution can cross through the equilibrium position (x = 0 ) at most once. Determine conditions on the initial position and velocity that allow the mass to pass through equilibrium.

Last modified: Wed Oct 8 08:23:52 EDT 1997