MA2051--C97 --- Solutions for TEST II
1.
(a)
The roots for the characteristic equation are -1 and 3/2, so
two solutions are e-t and e(3/2)
t. To verify independence,
compute the Wronskian and show that it is not zero.
(b)
Use the method of undetermined coefficients to find
yp(t) = 1/2
e-3t.
(c)
The general solution is
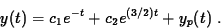
The initial data give c1 = -6/5 and
c2 = +6/5,
so y(t) = (6/5) e (3/2)t -
(6/5) e- t + (1/2)
e-3t.
(d)
For large values of t, the solution approaches the exponential term
(6/5)e(3/2)t -- everything else is transient. There is no
limiting periodic solution.
<\br><\br>
2.
(a)
The data give you m = 6 and k = (6)(9.8)/(0.02) = 2940,
so the model reduces to
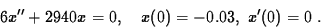
(b)
The characteristic equation has roots 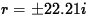 (approximately)
and so the general solution is
(approximately)
and so the general solution is
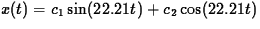 . The initial data
determine c1 = 0 and c2 = -0.03.
. The initial data
determine c1 = 0 and c2 = -0.03.
(c)
The amplitude is 0.03.
The period is 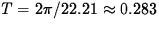 and it takes one half of
a period to travel from highest position to the lowest position.
and it takes one half of
a period to travel from highest position to the lowest position.
(d)
The velocity is 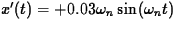 and
the mass passes through equilibrium at
and
the mass passes through equilibrium at 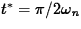 . The
velocity is therefore
. The
velocity is therefore 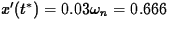 (meters per
second).
(meters per
second).
3.
(a)
The characteristic equation reduces to (r+4)(r-2) = 0 so the
roots are r1 = -4 and r2 = +2.
The first solution pair is (y1,z1) = (e-4t,3e-4t).
The second solution pair is (y2,z2) = (e2t,e2t).
(You can test linear independence with the Wronskian.)
The general solution is
(y,z) =
c1(y1,z1) +
c2(y2,z2).
(b)
The initial data gives 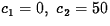 and so y= 50e2t, z= 50e2t.
(This is a straight line and the solution moves away from the origin
as t increases.)
and so y= 50e2t, z= 50e2t.
(This is a straight line and the solution moves away from the origin
as t increases.)
(c)
If you choose initial data so that the constants in the general
solution become 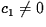 and c2 = 0, then you get convergence
to the origin; the solution becomes (y,z) = c1(e-4t, 3 e-4t).
(You must ``remove'' that nasty e+2t.)
Any initial data of the form y(0) = (1/3) z(0) works.
The solution curve in this case follows a straight line to the origin.
and c2 = 0, then you get convergence
to the origin; the solution becomes (y,z) = c1(e-4t, 3 e-4t).
(You must ``remove'' that nasty e+2t.)
Any initial data of the form y(0) = (1/3) z(0) works.
The solution curve in this case follows a straight line to the origin.
4.
The critical damping coefficient is p = 4 and the solution in this
case is
x(t) = xi e-2t + ( vi + 2xi) t e-2t
Set this equal to zero and solve for exactly one value:
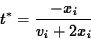
If xi > 0, this value of t is positive if and only if vi <
-2xi. (You have to push the mass
toward the origin to be sure it gets there.)
Arthur Heinricher <heinrich@wpi.edu>
Last modified: Wed Oct 8 08:36:08 EDT 1997
![]()
![]()
![]()