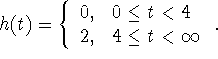MA2051 - Ordinary Differential Equations
Sample Exam 1 - B96
Second Exam - Originally Given 1993 A Term
Covers 5.1, 5.3, 6.1-6.6, 7.1, 7.2, 8.1-8.3, 11.1-11.4.
Instructions: Do your work on the paper provided. Put your
name and section number on that paper. Work neatly. Show your work.
JUSTIFY YOUR ANSWERS.
- 1 35 pts
- When a mass
of 200 gm is added to a spring, it deflects 8 cm.
- A
- Suppose a mass of 200 gm is suspended from this spring and
that the mass is started in motion from its equilibrium position
with a downward push of 6 cm/s. Write a model for the position
of the mass. (You don't need to derive the model from scratch.
Use the usual coordinate system: up is positive,
and the origin is the rest position of the mass.)
- B
- Find an expression for the position of the mass as a
function of time by solving the initial-value problem you wrote
in part (a).
- C
- Find the period of oscillation of the mass.
- D
- Find the maximum displacement of the mass.
- 2 20 pts
- Note that solutions
of x'' + 4x = 0 are
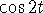 ,
, 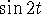 .
.
- A
- Find a particular solution of
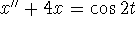 .
.
- B
- Find a general solution of this equation.
- C
- If this equation were a model of a spring-mass system, would
you conclude that the displacement of the mass is bounded or
unbounded? Give a physical reason for the behavior you observe.
- 3 25 pts
- Consider the
system
y' = -y + 3z
z' = 3y - z.
- A
- Find the characteristic values of this system.
- B
- Find a general solution of this system.
- C
- Find a solution that satisfies the initial conditions y(0) =
0, z(0) = 4.
This Topic will not be covered on the Exam
- 4 20 pts
- Define
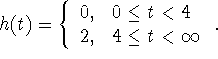
- A
- Find
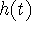 .
.
- B
- Find the Laplace transform of the solution of the
initial-value problem y' - y = h(t), y(0) = 4.
- C
- Find the solution of this initial-value problem.
© 1996 by Will Brother.
All rights Reserved. File last modified on December 6, 1996.
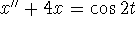 .
.