MA2051 - Ordinary Differential Equations
Sample Exam 2 Solutions - A96
Second Exam - Originally Given 1993 A Term
-
1
-
-
A
-
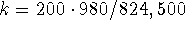 dynes/cm; the model is 200 x''
+ 24,500 x = 0, x(0) = 0, x'(0) = -6.
dynes/cm; the model is 200 x''
+ 24,500 x = 0, x(0) = 0, x'(0) = -6.
-
B
-
Use characteristic equations:
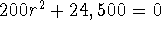 ;
; 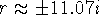 . Hence, a general solution is
. Hence, a general solution is 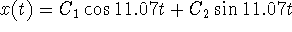 . The initial conditions force
. The initial conditions force 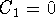 ,
C2 = -.06/11.07 = -.00542 . Hence,
,
C2 = -.06/11.07 = -.00542 . Hence, 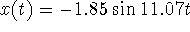 .
.
-
C
-
To find the period, solve
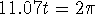 to find
to find 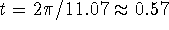 s.
s.
-
D
-
The maximum displacement occurs in
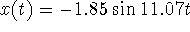 when the sine function is
when the sine function is 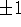 . Hence, the maximum
displacement (or amplitude of the motion) is 1.85 cm.
. Hence, the maximum
displacement (or amplitude of the motion) is 1.85 cm.
-
2
-
A
-
Use undetermined coefficients. First guess
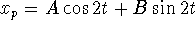 . Because these functions are solutions of the
homogeneous equation, the correct guess is
. Because these functions are solutions of the
homogeneous equation, the correct guess is 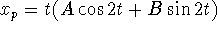 . Substitute and collect coefficients of sine and
cosine to find A = 0, B = 1/4. Hence,
. Substitute and collect coefficients of sine and
cosine to find A = 0, B = 1/4. Hence, 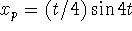 .
.
-
B
-
Using the particular solution just found and the
given homogeneous solutions,
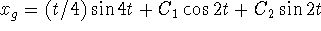 .
.
-
C
-
Because of the leading factor of t in
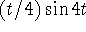 ,
the solution grows without bound. The system is being forced at
its resonant frequency.
,
the solution grows without bound. The system is being forced at
its resonant frequency.
-
3
-
-
A
-
r = -4, 2
-
B
-
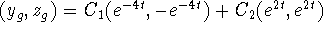 .
.
-
C
-
Choose
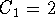 ,
, 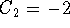 .
.
-
4
-
-
A
-
Write
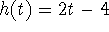 .
.
-
B
-
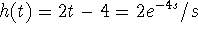
-
C
-
Let
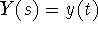 . Then
. Then 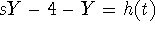 and
and
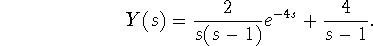
-
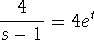 . Using partial fractions, we find
. Using partial fractions, we find
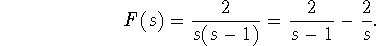
Then 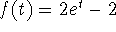 ,
, 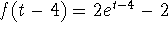 , and
, and
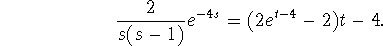
Hence, the solution is
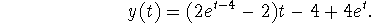
© 1996 by Will Brother.
All rights Reserved. File last modified on December 6, 1996.
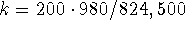 dynes/cm; the model is 200 x''
+ 24,500 x = 0, x(0) = 0, x'(0) = -6.
dynes/cm; the model is 200 x''
+ 24,500 x = 0, x(0) = 0, x'(0) = -6.
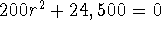 ;
; 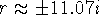 . Hence, a general solution is
. Hence, a general solution is 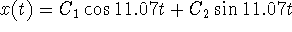 . The initial conditions force
. The initial conditions force 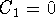 ,
C2 = -.06/11.07 = -.00542 . Hence,
,
C2 = -.06/11.07 = -.00542 . Hence, 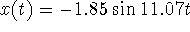 .
.
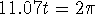 to find
to find 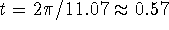 s.
s.
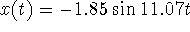 when the sine function is
when the sine function is 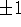 . Hence, the maximum
displacement (or amplitude of the motion) is 1.85 cm.
. Hence, the maximum
displacement (or amplitude of the motion) is 1.85 cm.
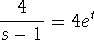 . Using partial fractions, we find
. Using partial fractions, we find