MA2051 - Ordinary Differential Equations
Sample Exam #3 - B96

Second Exam - Originally Given 1996 A Term 






Instructions: Do your work on the paper provided.  Put 
your name, section number and PLA's name on that paper.  Work 
neatly.  Show your work. JUSTIFY YOUR ANSWERS.





1 45 pts 

  A spring is 
suspended from a fixed support as shown in the figure.  In the 
coordinate system shown, an equation governing the motion of a mass m 
attached to this spring is my'' + ky = -mg.  The lower end of this 
particular spring settles to rest at y = -0.098 m when a mass of 
0.8 kg is hung from it.


    
      

    1.  Suppose a mass of 0.2 kg is suspended from the end of this 
    spring.  Write a model for the motion of the mass when it is 
    started by lifting it up to y = 0.1 m and releasing it from rest.

    2.  Find the period of oscillation of the 0.2 kg mass.  Would the 
    period of oscillation of the 0.8 kg mass be larger or smaller?

    3.  The governing equation has a steady state.  Find it and 
    explain carefully why it is physically reasonable.

    4.  If the mass were immersed in a fluid, its oscillations would 
    be damped, and the governing equation would have the form my'' + py' + 
    ky = -mg.  For what range of values of the damping coefficient p 
    will the 0.2 kg mass oscillate?  Would the 0.8 kg mass oscillate 
    over the same range of p values?

      
    










2 30 pts 

 Consider the 
system

  



    
      

    1.  Find its general solution.

    2.  Suppose y(0) = 2, z(0) = 4.  Use one step of Euler's 
    method to estimate y(3), z(3).

      
    










3 25 pts 

 


    
      

    1.  Find a general solution of y'' - 16y = 0.

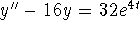    2.  Find a general solution of  tex2html_wrap_inline278 .

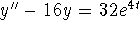    3.  Solve the initial-value problem  tex2html_wrap_inline278 , 
    y(0) = y'(0) = 0.

      
    
 
 

 





  

    

© 1996 by Will Brother.
All rights Reserved. File last modified on December 6, 1996.