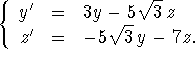MA2051 - Ordinary Differential Equations
Sample Makeup Exam - B96

Second Exam - Originally Given 1996 A Term 







1 45 pts 

  Recall the 
differential equation that governs the (small) oscillations of a mass m 
pivoted on a rod of length L:  tex2html_wrap_inline257 .


    
      

    1.  Write a model for the motion of a mass of 1.2 kg suspended 
    from a rod of length 2.45 m that is started in motion from a 
    vertical position with a push to the left of 0.1 radians/s.

    2.  What is the maximum angular displacement of the mass?

    3.  The mass was started in motion from the vertical position.  
    How much time will pass before it returns to vertical again?  If 
    the mass is increased to 2.0 kg, will that time increase or 
    decrease?

    4.  Suppose the rod stretches slightly.  Will the period of the 
    pendulum's oscillations increase or decrease?

    5.  In reality, friction in the pivot eventually stops the motion 
    of the pendulum.  A governing equation is 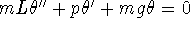 tex2html_wrap_inline259 ; p is the (small) damping coefficient.

      
    You want to design a pendulum that swings for as long as possible.  
    You can't change the pivot, but you can change both the length of 
    the rod and the size of the mass it supports.  What choice(s) will 
    minimize the effects of damping?

      
    










2 10 pts 

 Use one step of 
Euler's method to estimate the position and velocity at t = 0.5 s of 
the forced pendulum modeled by  tex2html_wrap_inline265 , 
 tex2html_wrap_inline267 ,  tex2html_wrap_inline269 .










3 20 pts 

 Find a general 
solution of  tex2html_wrap_inline271 









4 25 pts 

 


    
      

    1.  Find a general solution of y'' + 4y' - 96y = 0.

    2.  Find a general solution of y'' + 4y' - 96y = 24t.

      
    
 
 

 



  

    

© 1996 by Will Brother.
All rights Reserved. File last modified on December 6, 1996.