- 1
-
, 
,
.
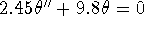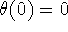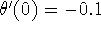Solve the preceding initial-value problem via characteristic equations:
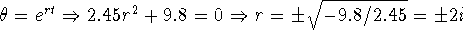. Hence, 
; 
;
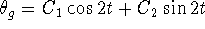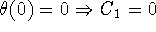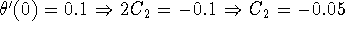. Since 
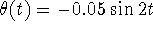, the maximum angular
displacement is 0.05 radians.
- 2
-
From the preceding solution formula, the period of the
pendulum is
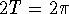or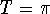 
s. The pendulum will first
return to vertical in half this time (it passes vertical
twice in each period) or in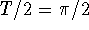 
s.
Since period is independent of mass, changing the mass will have no effect.
- 3
-
Repeating the analysis of part (b) with L in place of 2.45
m shows that
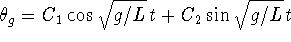. The period is 
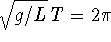or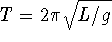 
. Hence, increasing L increases the period.
- 4
-
The characteristic equation of
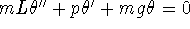is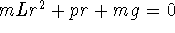 
. The characteristic roots
are
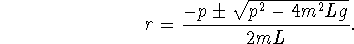
Since p is small and both m and L can be made large,
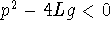; these roots are complex. Their real part is -p/2mL;
solutions of this differential equation will be damped by the
exponential factor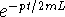 
. To minimize the effects of this
term, choose both m and L as large as possible.
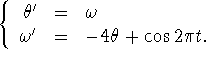Use 
, 
, 
. Then
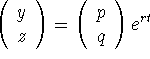leads to
.
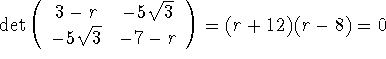When r = 8, choose p = 1 and find 
. When r =
-12, choose p = 1 and find 
. Hence,
: 
.
. Then 
forces -96 B = 24
or B = -1/4. Then 4 B - 96 A = 0 yields A = B/24 = -1/96 and
. Hence, 
.