MA2051 - Ordinary Differential Equations
Sample Exam #3 - Solutions


Second Exam - Orginally Given 1996 A Term 





    

  1. 

      

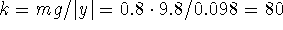    1.  Since  tex2html_wrap_inline279  N/m, the governing 
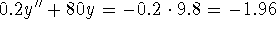    equation is  tex2html_wrap_inline281 , 
    y(0) = 0.1, y'(0) = 0.

    2.  The mass oscillates because 0.2 y'' + 80 y = 0 has a
    characteristic equation with pure imaginary roots: 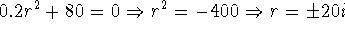 tex2html_wrap_inline289 .  The general 
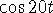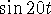    solution includes  tex2html_wrap_inline291  and  tex2html_wrap_inline293 .  The period of the 
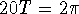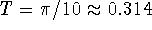    oscillations is  tex2html_wrap_inline295  or  tex2html_wrap_inline297  s.

      
    If m = 0.8, then 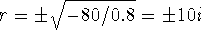 tex2html_wrap_inline301 .  The 
    natural frequency is reduced to 10 rad/s; the period increases 
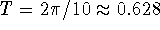    to  tex2html_wrap_inline303  s.

    3.  Since a steady state is constant, 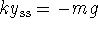 tex2html_wrap_inline305 , and 
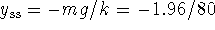     tex2html_wrap_inline307 .  This steady state is reasonable 
    because a) it is negative -- the spring sags when the weight 
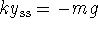    is added -- and because b)  tex2html_wrap_inline305  represents a 
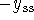    balance between the spring force due to the extension  tex2html_wrap_inline311  
    and the force of gravity -mg.

    4.  The mass oscillates so long as the characteristic equation of 
    my'' + p y' + k y = 0 has complex roots; i.e., so long as 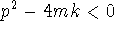 tex2html_wrap_inline317 .  Hence, oscillations are possible for  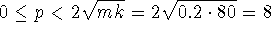tex2html_wrap_inline319  N-m/s.

      
    The 0.8 kg mass would oscillate over the same range of p 
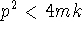    values as m = 0.2 kg because  tex2html_wrap_inline325  still holds 
    with m = 0.8 kg; or you could argue that m = 0.8 kg 
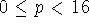    oscillates over a larger range of p values,  tex2html_wrap_inline333 .

      
    
    

    

  2.  

    
    
      

    1.  Characteristic equations yields r = -1, -4.  Substituting 
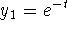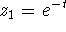     tex2html_wrap_inline337  in the first equation yields  tex2html_wrap_inline339 .  
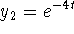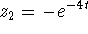    Substituting  tex2html_wrap_inline341  in the first equation yields  tex2html_wrap_inline343 .  A general solution is
    
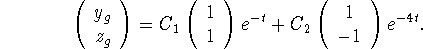
       displaymath277 
      

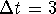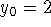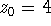    2.  Use  tex2html_wrap_inline345 ,  tex2html_wrap_inline347 ,  tex2html_wrap_inline349 : 
    
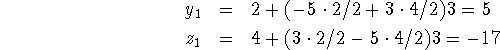
       eqnarray268 
    

    

  3.  

    
    
      

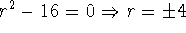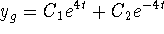    1.  Characteristic equations:  tex2html_wrap_inline351 .  Hence,  tex2html_wrap_inline353 .

    2.  Need a particular solution.  Use undetermined coefficients: 
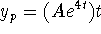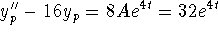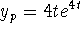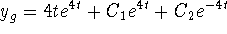     tex2html_wrap_inline355 .  Find  tex2html_wrap_inline357  forces A = 4 and  tex2html_wrap_inline361 .  Hence,  tex2html_wrap_inline363 .

    3.  Use the initial conditions in the previous general solution 
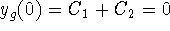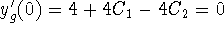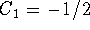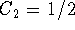    to find  tex2html_wrap_inline365 ,  tex2html_wrap_inline367 .  Hence,  tex2html_wrap_inline369 ,  tex2html_wrap_inline371 , and the solution of the 
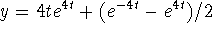    initial-value problem is  tex2html_wrap_inline373 .