See the accompanying figure. For simplicity, suppose the spring
obeys Hooke's Law with constant K and that the car-spring system is
damped by a friction force proportional to velocity. Typically, a car
might have a mass of about M = 1,000 kg and be traveling about 30 m/s
( 
mph) when it hits the bumper.
- A
- Using the coordinate system indicated in the diagram, write
an expression for the force of the spring on the car when it is
located at position x.
- B
- Derive from Newton's Law a model of the form
.
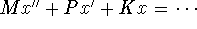- C
- Is the equation in your model linear or nonlinear?
Homogeneous or nonhomogeneous?
- D
- What range of values of K would guarantee that the system
does not oscillate after a collision? Do these values
correspond to a weaker or a stronger spring?
- E
- Suppose the road is covered with ice so there is no damping
from friction. What value of the spring constant K would limit
the deflection of the car-spring system to 2 m?
