MA2051 - Ordinary Differential Equations
Solutions to Sample Exam 2 - B96
Second Exam - Originally Given 1995 D Term
-
1
-
-
A
-
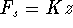 , z = -x,
, z = -x, 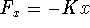
-
B
-
;
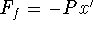 ; M x'' = -Kx - Px'. With
initial conditions, the final model is Mx'' + Px' + Kx = 0, x(0)
= 0, x'(0) = 30.
; M x'' = -Kx - Px'. With
initial conditions, the final model is Mx'' + Px' + Kx = 0, x(0)
= 0, x'(0) = 30.
-
C
-
The equation is linear and homogeneous.
-
D
-
Preventing oscillations requires real characteristic roots:
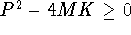 . Hence, no oscillations if
. Hence, no oscillations if 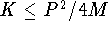 ; the
spring can not be too strong lest the system oscillate.
; the
spring can not be too strong lest the system oscillate.
-
E
-
Solve Mx'' + Kx = 0, x(0) = 0, x'(0) = 30 to find
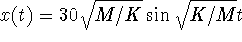 . Maximum displacement (or
amplitude) of
. Maximum displacement (or
amplitude) of 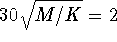 occurs with
occurs with 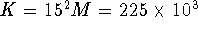 N/m.
N/m.
-
2
-
-
A
-
Via characteristic equation:
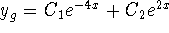
-
B
-
Combine previous homogeneous solution with undetermined
coefficients using
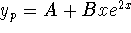 :
: 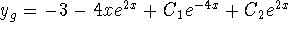
-
C
-
Via characteristic equation:
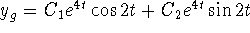
-
D
-
Combine previous homogeneous solution with undetermined
coefficients using :
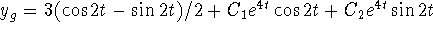
-
E
-
section 8.2, exercise 7
© 1996 by Will Brother.
All rights Reserved. File last modified on December 6, 1996.
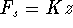 , z = -x,
, z = -x, 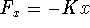
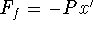 ; M x'' = -Kx - Px'. With
initial conditions, the final model is Mx'' + Px' + Kx = 0, x(0)
= 0, x'(0) = 30.
; M x'' = -Kx - Px'. With
initial conditions, the final model is Mx'' + Px' + Kx = 0, x(0)
= 0, x'(0) = 30.
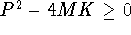 . Hence, no oscillations if
. Hence, no oscillations if 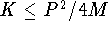 ; the
spring can not be too strong lest the system oscillate.
; the
spring can not be too strong lest the system oscillate.
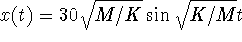 . Maximum displacement (or
amplitude) of
. Maximum displacement (or
amplitude) of 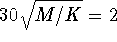 occurs with
occurs with 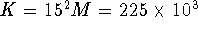 N/m.
N/m.