E97 Final Exam Solutions, MA 2051

Exam given in term E97, July 24, 1997: Solutions

Post-script version

1.

Solve the initial value problems

(a)

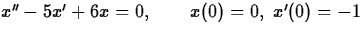$x'' - 5x' + 6x = 0,\qquad x(0) = 0,\; x'(0) = -1$ .The characteristic equation, r² - 5r + 6=0 has roots 2,3.

The general solution is x_g = C₁ e^2t + C₂ e^3t.

The initial conditions require C₁ = 1 and C₂ = -1. Therefore,

x(t) = e^2t - e^3t

(b)

$x'' + 4x = 8\sin(2t),\qquad x(0) = 0,\; x'(0) = 0$ .

The general solution to the homogeneous solution is

$\begin{displaymath} x(t) = C_1\cos(2t) + C_2\sin(2t). \end{displaymath}$

The particular solution has the form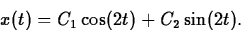

$\begin{displaymath} x_p(t) = (A\cos(2t)+B\sin(2t))t \end{displaymath}$

That gives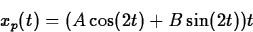

$\begin{displaymath} x_p'' + 4x_p = -4A\sin(2t) + 4B\cos(2t) \end{displaymath}$

so A=-2 and B=0.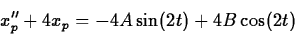

Therefore, the general solution to the nonhomogeneous equation is

$\begin{displaymath} C_1\cos(2t) + C_2\sin(2t) - 2t\cos(2t) \end{displaymath}$

The initial conditions require C₁ = 0 and C₂ = 1.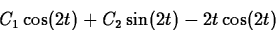

Therefore, the solution to the initial-value problem is

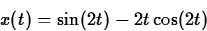
$\begin{displaymath} x(t) = \sin(2t) - 2t\cos(2t) \end{displaymath}$

2.

For the differential equation $x'' + 6x' + 13x = 4\sin(2t)$

(a)

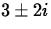Find the general solution to this equation. The roots of the characteristic equation are $3\pm 2i$ .

The general solution to the homogeneous equation is

$\begin{displaymath} e^{-3t}(C_1\cos(3t)+C_2\sin(3t)) \end{displaymath}$

The particular solution has the form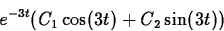

$\begin{displaymath} x_p = A\sin(2t) + B\cos(2t) \end{displaymath}$

The method of undetermined coefficients gives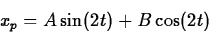

$\begin{displaymath} A = \frac{4}{25};\qquad B = \frac{16}{75} \end{displaymath}$

The general solution is therefore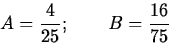

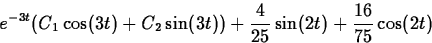
$\begin{displaymath} e^{-3t}(C_1\cos(3t)+C_2\sin(3t))+ \frac{4}{25}\sin(2t)+\frac{16}{75}\cos(2t) \end{displaymath}$

(b)

What part of the solution will become unimportant after a long time (the transient)? What part of the solution will be important after a long time (the limiting behavior)?

The transient is

$\begin{displaymath} e^{-3t}(C_1\cos(3t)+C_2\sin(3t)) \end{displaymath}$

The limiting solution is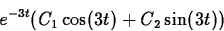

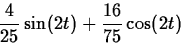
$\begin{displaymath} \frac{4}{25}\sin(2t) + \frac{16}{75}\cos(2t) \end{displaymath}$

(c)

Find the amplitude and period of the limiting solution

The amplitude is

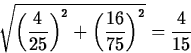
$\begin{displaymath} \sqrt{\left(\frac{4}{25}\right)^2 + \left(\frac{16}{75}\right)^2} = \frac{4}{15} \end{displaymath}$

3.

Write a differential equation that models a spring-mass system with mass 1 kg, damping coefficient 5 kg/s, and a spring constant 4 N/m. Is the system underdamped or overdamped? Using the same damping coefficient and spring constant, what mass will make the system critically damped?

The differential equation is

x'' + 5x' + 4x = 0

The characteristic equation, r² + 5r + 4 = 0, has real roots -1,-5 so the system is overdamped.

The characteristic equation for general mass m is

mr² + 5r + 4 = 0,

has discriminant 25-16m. The system is critically damped when

$\begin{displaymath} m = \frac{25}{16}\end{displaymath}$

4.

For the first-order equation y' = y² - 3y, where are the equilibria? For each equilibrium, determine if it is stable or if it is unstable.

The equilibria are the roots of y² - 3y, or y=0 and y=3.

y²-3y>0 if y>3 or y<0, and y² - 3y<0 if 0<y<3.

Therefore solutions are

increasing ( $\nearrow$ ) if y>3
decreasing ( $\searrow$ ) if 0<y<3
increasing ( $\nearrow$ ) if y<0

So the equilibrium at y=3 is unstable and the equilibrium at y=0 is stable.

Alternate solution to the question of stability:

The linearization about y=0 is y' = -3y. The linearized equation is stable at y=0, so the original equation is stable at y=0.

Linearize about y=3: Put y=3 + p; then y² - 3y = 3(y-3)+(y-3)² so p' = 3p + p². The linearization around y=3, or p=0, is p' = 3p, which has an unstable equilibrium.

Therefore the original equation is unstable at y=3.

Nathan Gibson
12/11/1997