MA2051--C97Name

TEST ISection Instructions: Do your work on the paper provided. Put your name and section number on the cover and on each page. Work neatly and show your work. Remember, your work and explanations are graded, not just the final answer. 1. (35 points) In this problem, you will analyze the following linear differential equation:

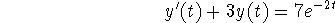
(a)

Find a nontrivial solution for the corresponding homogeneous equation.

(b)

Find a particular solution for the original differential equation.

(c)

Find the solution for the differential equation which satisfies the initial condition y(0) = 5.

(d)

Can you choose the initial condition so that the solution to the initial value problem contains only the particular solution? Explain your answer clearly.

2. (35 points) The Worcester Yeast Company also makes soft drinks. The company has a 1000 gallon tank that it uses to mix sugar-water. Two pipes pour different liquid sugar concentrates into the tank. The first pipe pumps concentrate containing 6 tablespoons per gallon into the tank at the rate of 2 gallons per minute. The second pipe pumps concentrate containing 10 tablespoons per gallon into the tank at a rate of 1 gallon per minute. Assume that the volume of solution in the tank is kept constant (and equal to 1000 gallons).

Let A(t) denote the amount of sugar in the tank at time t. Let C(t) denote the concentration of sugar in the tank at time t.

(a)

Write an expression for the rate at which sugar is entering the tank.

(b)

Write an expression for the rate at which sugar is leaving the tank.

Why is it important to assume that the liquid in the tank is ``thoroughly mixed'' before the mixture is removed from the room?

(c)

Write a balance equation that relates the net change in the amount of sugar in the tank over a time 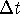with the rate at which it is added and lost. Use this equation to derive a differential equation for the amount of sugar in the tank at time t. (Do not solve the differential equation.)

(d)

If you wait a long time, the concentration in the mixture flowing out of the tank will be constant. Use your model to predict this constant level.

3. (15 points) The following equation models a population that grows faster than the standard exponential model:

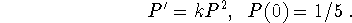
Solve the equation and show that the population will become infinite in finite time. 4. (15 points) Work with the following differential equation:

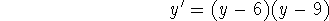
(a)

Find all of the steady states for this equation.

(b)

Determine the regions in the (t,y) plane where the solution curves are increasing and where the solution curves are decreasing.

(c)

Sketch solution curves starting at three different initial points: y(0) = 0, y(0) = 8.9, and y(0) = 12.

Bonus The logistic equation

is a nonlinear equation. Show that a new variable defined by

satisfies a linear equation. Use this linear equation to solve the original logistic equation. Explain your answer completely.

• About this document ...