MA2051--C97SOLUTIONS FOR TEST I 1. You are solving

(a)

The corresponding homogeneous equation is . The characteristic equation is r +3 = 0, so r=-3 and the homogeneous solution is .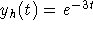

(b)

Use the method of Undetermined Coefficients and look for a solution of the form 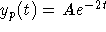. Plug this into the original equation and equate coefficients to obtain A = 7, so .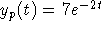

(c)

The general solution is 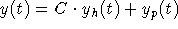. The initial condition gives you 5 = y(0) = C + 7 and so C = -2.

(d)

The answer is yes: simply choose 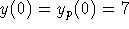(and remember that solutions are unique).

2. Let A(t) denote the amount of sugar (in Tbsp) in the tank at time t and let C(t) denote the concentration of sugar in the tank at time t (in tablespoons per gallon). Then C(t) = A(t)/V = A(t)/1000.

(a)

Sugar enters the tank at rate 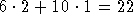(Tbsp/min).

(b)

Sugar leaves the tank at the rate 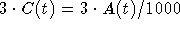(Tbsp/minute). The assumption that the tank is ``well-mixed'' implies that the concentration of sugar is uniform throughout the tank.

(c)

The balance equation is Net change between t and

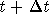
= (rate in) 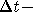(rate out) ,

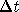or

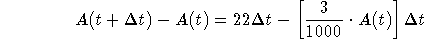
Collect terms, divide by 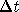and take the limit as 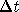approaches zero to obtain the model:

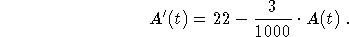
(d)

The equation has a steady state at 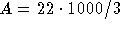, so the concentration will be close to C = 22/3 = 7.333 if you wait long enough.

3. Just separate and integrate:

gives you

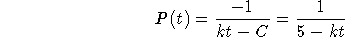
when you plug in the initial data.

The disaster occurs as t approaches 5/k, when the population becomes larger than the number of electrons in the universe.

4. The differential equation tells you that The steady states are y=+6 and y=+9, where .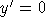

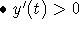when (or where) y(t) < 6 or y(t)> 9

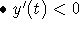when 6 < y(t) < 9

Your graph starting at y=0 should increase, be concave down, and have a horizontal asymptote at y=6. The graph starting at y=12 should be increasing and concave up. The graph starting at y=8.9 should decrease, be concave down initially but switch to concave up (at y=7.5), and have a horizontal asymptote at y=6. Bonus Problem Define Q(t) = 1/P(t) and differentiate it:

but this simplifies to

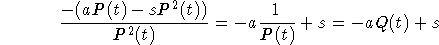
This is linear for Q and the solution is

• About this document ...