MA2051 - Ordinary Differential Equations
Sample Exam Questions - C97
Originally Given 1996 D Term
Instructions: Do your work on the paper provided. Put your
name and section number on the cover and on each page.
Remember, your work and explanations are graded, not just the
final answer.
1. (30 points) In solving the following problems,
be sure to use work from previous parts if you can.
As always, you must justify your answers.
- (a)
-
Find two linearly independent solutions
for
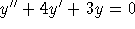 . Prove that your solutions really are linearly independent.
. Prove that your solutions really are linearly independent.
- (b)
-
Find a particular solution for
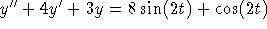 .
. - (c)
-
Find the solution for
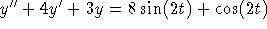 which satisfies
which satisfies 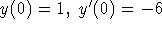 .
.
2. (30 points)
Work with the following model for a damped, unforced spring:
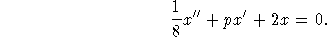
- (a)
-
When there is no damping (so p=0)
you can assume that the general solution is of the
form
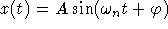 where
where 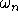 is
the natural frequency.
Find the constants
is
the natural frequency.
Find the constants 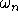 , A and
, A and 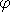 for the motion if
the mass is pulled down 6 cm and released from rest.
for the motion if
the mass is pulled down 6 cm and released from rest.
- (b)
-
When the motion of the mass is opposed by a friction
damping force (so p > 0), the general solution is not
the same as in part (a).
Find the smallest value for p that would eliminate
all oscillations from the solution. (Note: you do not
have to actually solve the differential equation to answer this
question.)
- (c)
-
Find the smallest damping coefficient p > 0 that will reduce
oscillations with an initial amplitude of 6 cm to an
amplitude of 0.01 cm in 60 seconds.
Explain your method clearly.
3. (30 points)
Consider the following initial value problem:
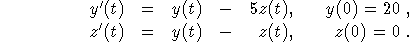
-
(a)
-
Give the characteristic equation and find its roots.
Find two linearly independent solution pairs and use them to
obtain the general solution for the system.
- (b)
-
Find the solution satisfying the given initial conditions.
- (c)
-
Sketch the solution curves for at least three initial points
in the (y,z)-plane. Indicate clearly the direction of
motion along the curve as t increases.
4. (10 points)
Define the total energy of an unforced,
damped (with damping coefficient p>0) spring-mass system by
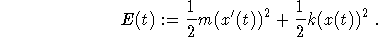
Use the standard model for a damped spring to
compute 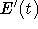 and show that it is strictly negative
(whenever the spring is moving) and so the energy is always decreasing.
and show that it is strictly negative
(whenever the spring is moving) and so the energy is always decreasing.
© 1997 by MA2051 Webmasters
All rights Reserved. File last modified on February 27, 1997
![]()
![]()
![]()
![]() and show that it is strictly negative
(whenever the spring is moving) and so the energy is always decreasing.
and show that it is strictly negative
(whenever the spring is moving) and so the energy is always decreasing.