MA2051 - Ordinary Differential Equations
First Sample Exam Questions - C97

Originally Given 1994 B Term 




Instructions:  Do your work on the paper provided.  Put your
name and section number on the cover and on each page.  Work neatly
and show your work.  
Remember, your work and explanations are graded, not just the 
final answer. 


1. (40 points) 
Work with the following linear differential equation.  

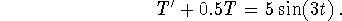
 displaymath18 


(a)

 
Find a nontrivial solution for the corresponding homogeneous equation.  

(b)

 
Find a particular solution for the original differential equation.

(c)


Find the general solution as well as the solution satisfying the 
initial condition T(0) = 32. 

(d)


Is it possible to choose the initial value 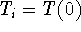 tex2html_wrap_inline48  so that
the solution to the initial value problem 
is exactly equal to the particular solution 
found in part (b)?  If it is not possible, explain why not.  If it is 
possible, explain how to do it.


 



2. (25 points)  
Solve each of the following initial value problems:

 displaymath23 



3. (35 points) 
Water containing 2 oz of TCE (a toxic waste) per gallon flows into a 
treatment tank at a rate of 500 gallons per minute.  The volume of the tank is
fixed at 10,000 gallons (so water must flow out at the same rate that
it flows in). 
The treatment process is able to remove 12% of the current amount
of TCE in the tank per minute.
Assume that the water is thoroughly stirred and 
that the tank is initially filled with clean water.



(a)


Write an expression for the rate at which TCE is 
added to the tank. 
Write an expression for the rate at which TCE
is removed from the tank.  
Define all of the variables used in your expressions. 
(Note: TCE is removed by treatment as well as the out-flow.)

(b)

 
Write a balance equation reflecting the fact that 
the net change in the amount of TCE in the tank over a 
time 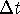 tex2html_wrap_inline50  is equal to the amount of TCE added minus
the amount of TCE removed.  
Use this law and the results from part (a) to derive
a differential equation model for the amount of TCE in the tank
at time t.  (Do not solve the initial value problem.)

(c)


If you wait a long time (like 24 hours), the 
concentration of TCE in the water flowing out of the tank
approaches a constant level. 
Without solving the differential equation derived in part (b),
determine this constant level. 

(d)

  
Use your model (and the results from part (c)) to determine
ways to reduce the concentration of TCE in the water
flowing out of the tank.  Justify your answer.


 



4: BONUS  (5 points)
Government regulations specify that the maximum allowed TCE concentration
released from the tank is 0.05 oz per gallon.
Change the parameters in the model if you need to, but
find a way to satisfy the government regulations (or go out of business).





  

    

© 1997 by MA2051 Webmasters

All rights Reserved. File last modified on January 31, 1997