MA2051 - Ordinary Differential Equations
Solutions to first sample exam

Originally Given 1994 B Term 





1. 
You are solving 

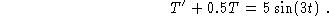
 displaymath10 




(a)

 
The corresponding homogeneous equation is 
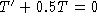 tex2html_wrap_inline59 . 
The characteristic equation is r + 0.5 = 0, and so r=-0.5
and the homogeneous solution is 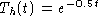 tex2html_wrap_inline65 . 

(b)

 
Use the method of Undetermined Coefficients and look for a solution of
the form
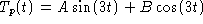 tex2html_wrap_inline67 .  Plug this into the original
equation and equate coefficients to obtain
 A = 10/37 and B = -60/37.  

(c)


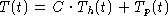The general solution is  tex2html_wrap_inline73 .
The initial condition gives you 32 = T(0) = C - 60/37 and
so C = 32 + 60/37.  

(d)


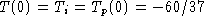The answer is yes: simply choose  tex2html_wrap_inline79 .
(You just have to make the initial data match the initial
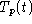value for  tex2html_wrap_inline81 .)


 



2. 
(a) Separate and integrate:

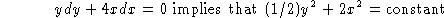
 displaymath83 

The initial data determines the constant to be 26.  (The solution is
the top half of an ellipse.)


(b) Separate and integrate again:

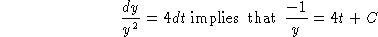
 displaymath85 

Use the initial data and simplify to obtain
 y = 1/(12-4t)




3. 
Let A(t) denote the amount of TCE in the tank at time t (in ounces)
and let C(t) denote the concentration of TCE in the tank at time t 
(in ounces per gallon).  Then C(t) = A(t)/V = A(t)/10,000.



(a)


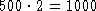TCE enters the tank at rate  tex2html_wrap_inline99  (ounces/minute).
There are two ways that TCE ``leaves'' the tank: in the water flowing 
out and through treatment.  
The rate out due to flow is 
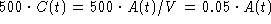 tex2html_wrap_inline101  (ounces/minute).
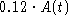The rate out due to treatment is  tex2html_wrap_inline103  (ounces/minute).



(b)

 
The balance equation is

 displaymath105 

Collect terms, divide by 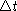 tex2html_wrap_inline107  and take the limit as
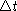 tex2html_wrap_inline107  approaches zero to obtain the model:

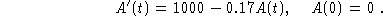
 displaymath111 




(c)


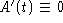If you are going to have a constant solution, then  tex2html_wrap_inline113 
and the model tells you that this happens when 1000 - 0.17A(t) = 0.
Thus the amount of TCE in the tank approaches the constant level
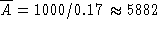 tex2html_wrap_inline117  ounces and so the concentration
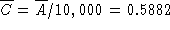approaches the constant level  tex2html_wrap_inline119  
(ounces per gallon).  
This is the concentration of TCE in the water flowing out of the tank.



(d)

  
There are (at least) three ways to reduce the concentration of TCE in
the water leaving the tank: reduce the flow rate, 
increase the size of the tank, increase the efficiency of the 
treatment process.


If you go back to the model, and let 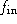 tex2html_wrap_inline121  denote the flow rate in
(as well as out), let V denote the volume, and r denote the
treatment rate, the model becomes

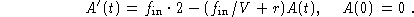
 displaymath127 

You can solve for the constant solution as before, and you find
that the concentration approaches the constant level

 displaymath129 

In other words, the treatment tank multiplies the in-flow concentration by
the fraction 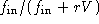 tex2html_wrap_inline131 .  You want to make this fraction  small
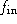and you can do that by (1) decreasing  tex2html_wrap_inline121 , or (2) increasing V,
or (3) increasing r.


 



4: BONUS  
If you want to stay in business, you need 
 
 displaymath139 
  
One way to attain this is to
keep V=10,000, r = 0.12 and decrease the flow rate 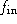 tex2html_wrap_inline121 .  If you
do this you find that the maximum admissible flow rate is about 30.77
gallons per minute.  (Slow flow.)


Another way to do it is to keep the flow rate equal to 500 gallons/minute,
but increase the volume of the tank.  If you want to do this, you need a tank
with volume 162,500 gallons.  (Big tank.)


It is interesting to note that you cannot satisfy the government
regulations even if the treatment is 100% efficient; r=1 isn't
good enough!





  

    

© 1997 by MA2051 Webmasters

All rights Reserved. File last modified on January 31, 1997