MA2051 - Ordinary Differential Equations
Sample Exam
Orginally Given 1996 D Term
Instructions: Do your work on the paper provided. Put your
name and section number on the cover and on each page. Work neatly
and show your work.
Remember, your work and explanations are graded, not just the
final answer.
1.
(20 points)
Solve each of the following initial value problems:

2. (35 points)
In this problem, you will analyze the following linear
differential equation:
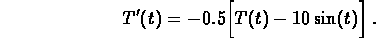
- (a)
-
Find a nontrivial solution for the corresponding homogeneous equation.
- (b)
-
Find a particular solution for the original differential equation.
- (c)
-
Find the solution for the differential equation which
satisfies the initial condition
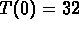 .
.
- (d)
-
Can you choose the initial condition so that the solution to the
initial value problem contains only the particular solution?
Explain your answer clearly.
3. (35 points)
A large lecture hall containing 40,000 cubic meters of air
is originally free of carbon monoxide.
Beginning at time t=0, smoke containing 3% carbon monoxide
begins leaking into the hall at the rate of 2 cubic meters per minute.
The ventilation system removes the mixture of air
and smoke from the hall at the same rate (2 cubic meters per minute).
- (a)
-
Write an expression for the rate at which
carbon monoxide is entering the room.
- (b)
-
Write an expression for the rate at which
carbon monoxide is leaving the room.
(Your expression should depend on the concentration
of carbon monoxide in the room at time t.)
Why is it important to assume that the smoke and
air are ``thoroughly mixed'' before the mixture
is removed from the room?
- (c)
-
Write a balance equation that relates the
net change in the amount of carbon monoxide in the hall
over a time
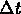 with the rate at which it is added
and lost.
with the rate at which it is added
and lost.
- (d)
-
Use the results from parts (a), (b) and (c) to
derive a differential equation model for the concentration
of carbon monoxide in the lecture hall at time t.
(Do not solve the differential equation.)
4. (10 points)
The differential equation in Problem 2 models heat-loss
with a non-constant outside temperature (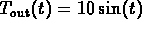 ).
Make a rough sketch of the solution curve for this model
with initial data
).
Make a rough sketch of the solution curve for this model
with initial data 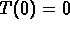 .
Does the inside temperature oscillate with the same
range as the outside temperature (
.
Does the inside temperature oscillate with the same
range as the outside temperature (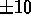 degrees)?
(Hint: You don't need the solution formula.
Sketch the outside temperature first and determine
where
degrees)?
(Hint: You don't need the solution formula.
Sketch the outside temperature first and determine
where 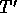 is positive, negative, and zero.)
is positive, negative, and zero.)
Explain why it is not possible for the solution curve to
follow the 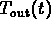 exactly.
exactly.
© 1997 by MA2051 Webmasters
All rights Reserved. File last modified on January 31, 1997


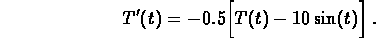
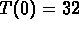 .
.
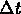 with the rate at which it is added
and lost.
with the rate at which it is added
and lost.
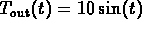 ).
Make a rough sketch of the solution curve for this model
with initial data
).
Make a rough sketch of the solution curve for this model
with initial data 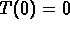 .
Does the inside temperature oscillate with the same
range as the outside temperature (
.
Does the inside temperature oscillate with the same
range as the outside temperature (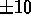 degrees)?
(Hint: You don't need the solution formula.
Sketch the outside temperature first and determine
where
degrees)?
(Hint: You don't need the solution formula.
Sketch the outside temperature first and determine
where 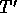 is positive, negative, and zero.)
is positive, negative, and zero.)
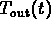 exactly.
exactly.