1.
- (a) Just integrate:
-
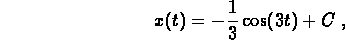
and use the initial data:
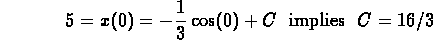
- (b)
-
Separate

integrate and simplify to obtain

Use the initial data to find C:
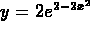
2. You are solving
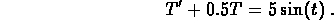
- (a)
-
The corresponding homogeneous equation is
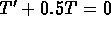 .
The characteristic equation is
.
The characteristic equation is 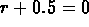 , and so
, and so 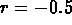 and the homogeneous solution is
and the homogeneous solution is 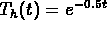 .
.
- (b)
-
Use the method of Undetermined Coefficients and look for a solution of
the form
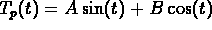 . Plug this into the original
equation and equate coefficients to obtain
A = 2 and B = -4.
. Plug this into the original
equation and equate coefficients to obtain
A = 2 and B = -4.
- (c)
-
The general solution is
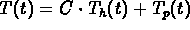 .
The initial condition gives you
.
The initial condition gives you 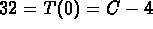 and
so C = 36.
and
so C = 36.
- (d)
-
The answer is yes: simply choose
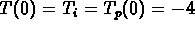 .
(You just have to make the initial data match the initial
value for
.
(You just have to make the initial data match the initial
value for 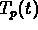 .)
.)
3. Let
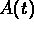 denote the amountof carbon monoxide
in the lecture hall at time t (in cubic meters)
and let
denote the amountof carbon monoxide
in the lecture hall at time t (in cubic meters)
and let 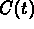 denote the concentrationof
carbon monoxide in the hall at time t
(in cubic meters per cubic meter).
Then
denote the concentrationof
carbon monoxide in the hall at time t
(in cubic meters per cubic meter).
Then 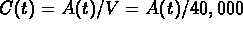 .
.
- (a)
-
CO enters the hall at rate
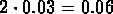 (
(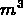 /minute).
/minute).
- (b)
-
CO leaves the hall at the rate
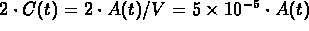 (
(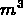 /minute).
/minute).
- (c)
-
The balance equation is
Net change in the amount between t and
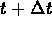 = (rate in)
= (rate in) (rate out)
(rate out)  ,
,
or
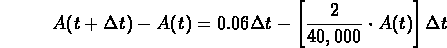
- (d)
-
Collect terms, divide by
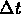 and take the limit as
and take the limit as
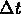 approaches zero to obtain the model:
approaches zero to obtain the model:
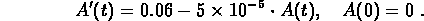
To turn this into an equation for the concentration, replace
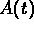 by
by 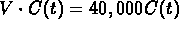 everywhere that you see it.
everywhere that you see it.
4. Sketch the graph of
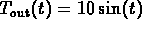 .
The differential equation tells you
.
The differential equation tells you
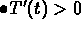 when (or where)
when (or where) 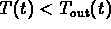
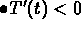 when
when 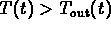
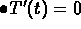 when
when 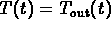
The last condition tells you that the inside temperature
can have a max or a min only when the the solution curve
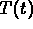 crosses the graph of
crosses the graph of 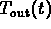 .
It also tells you that
.
It also tells you that 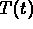 cannot follow
cannot follow 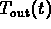 exactly (because
exactly (because 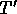 would have to be zero everywhere along the
solution).
would have to be zero everywhere along the
solution).
For the initial data given 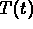 starts at 0 and stays
strictly below
starts at 0 and stays
strictly below 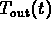 until the curves cross
(at some time after
until the curves cross
(at some time after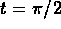 when
when 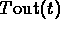 is strictly less than 10). This shows that
the amplitude of th inside temperature is smaller than
the amplitude of the outside temperature.
is strictly less than 10). This shows that
the amplitude of th inside temperature is smaller than
the amplitude of the outside temperature.
© 1996 by MA2051 Webmasters All rights Reserved. File last modified on