MA2051 - Ordinary Differential Equations
Project 2b - Nonlinear Resistance - C97

You have seen in lecture and exercises how to model a forced spring-mass system with damping. The mathematical model for the charge on the capacitor in an LRC circuit is exactly the same:

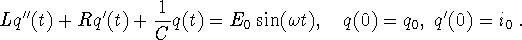
1. Second-order differential equations can be rewritten as systems of first-order equations. Take 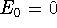(so there is no source term) and verify that the differential equation given above can be rewritten as

   

   Plot some solution curves for this model in the (I,V) plane. For simplicity (and sanity), choose parameter values C=1 and L=1. How do the solutions change with R?

2. It is possible to design a circuit that will produce a periodic output current even when there is no source term. Circuits such as these were developed for the first commercial radios in the 1920's. Balthazar van der Pol designed a circuit in which the passive resistor is replaced by an active element which would pump energy into the circuit whenever the amplitude of the current falls below a certain level. (In the 1920's, these active elements were vacuum tubes.) In the van der Pol circuit, the potential drop across the active element (which used to be just RI) is given by a nonlinear function such as .

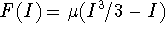   Do some numerical studies of the van der Pol circuit. For simplicity, take C=1 and L=1 as in the last part. Focus on how the solution changes for different values of the parameter .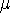

3. The resulting limit cycles are sometimes called relaxation oscillations. Can you explain this terminology? (You may want to visit your favorite, and most relaxed, electrical engineer. In particular, it is important to look at how fast the solution moves through different parts of the solution curve.)

Final Version Due: Thursday, March 6