Solutions to Midterm Exam given in term B97, November 18, 1997

Post-script version

1.
(20 points) Solve each of the following initial-value problems:
a.
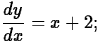$\displaystyle{\frac{dy}{dx}=x + 2};$ y(2) = 3. Integrating,

\begin{displaymath} y = \frac{1}{2}x^2 + 2x + C\end{displaymath}

Substituting in the initial value,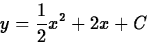

\begin{displaymath} 3 = 6 + C\Longrightarrow C = -3\end{displaymath}

The solution is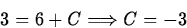

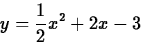
\begin{displaymath} y = \frac{1}{2}x^2 + 2x - 3 \end{displaymath}

b.
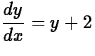$\displaystyle{\frac{dy}{dx}=y + 2}$; y(2) = 3. The general solution is

y = -2 + Cex

Substituting in the initial value,

\begin{displaymath} 3 = -2 + Ce^2 \Longrightarrow C = 5e^{-2} \end{displaymath}

The solution is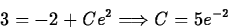

y = -2 + 5ex-2

2.
(30 points) Consider the differential equation

\begin{displaymath} \frac{dx}{dt} = 4x - 5\cos(2t)\end{displaymath}

a.
Find a nontrivial solution to the homogeneous equation. The homogeneous equation is x' = 4x; therefore

xh = e4t

is a homogeneous solution.

b.
Find a particular solution to the differential equation Try to find a solution of the form

\begin{displaymath} x_p = A\cos(2t) + B\sin(2t)\end{displaymath}

Substituting,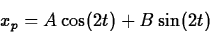

\begin{displaymath} -2A\sin(2t)+2B\cos(2t)=4A\cos(2t)+4B\sin(2t)-5\cos(2t)\end{displaymath}

Grouping sines and cosines,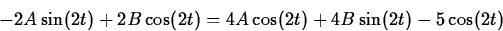

Solving gives A = 1 and B = -1/2. Therefore

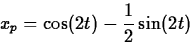
\begin{displaymath} x_p = \cos(2t) - \frac{1}{2}\sin(2t)\end{displaymath}

c.
Find the general solution to the equation.

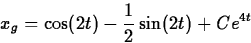
\begin{displaymath} x_g = \cos(2t) - \frac{1}{2}\sin(2t) + Ce^{4t}\end{displaymath}

d.
Consider the solutions with two different initial values. Do the solutions get farther apart or closer together as t increases? Justify your answer.

The solutions will be

for two different constants C1 and C2.

Their difference is

x2(t)-x1(t) = (C2-C1)xh(t) = (C2-C1)e4t

Since the exponential gets large as t gets large, the solutions get further apart.

3.
(30 points) Water is being poured into a tank at a constant rate of 3 liters per second. A small leak at the bottom of the tank causes water to leak out at a rate proportional to the amount of water in the tank. Suppose that initially there is 400 liters of water in the tank and that initially the leaking rate is 4 liters per second.

a.
Write an expression for the amount of water that is added to the tank in a small time period. Write an expression for the amount of water that leaves the tank in the same small time period. Define any variables you use.

Define:

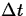$\Delta t$:
length of small time period
V:
volume of water
k:
proportionality constant between leakage and volume (leakage rate = kV)
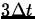Amount added is $3\Delta t$.
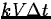Amount lost is $kV\Delta t$.

But initially, V = 400 and the rate of leakage is 4, so k = 0.01.

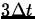Amount added is $3\Delta t$.
Amount lost is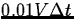 $0.01V\Delta t$.

b.
Write an equation that gives the change in the amount of water over a small time period. Use this equation to create a differential equation model for the amount of water in the tank as a function of time.

Change over 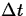$\Delta t$ is

\begin{displaymath} \Delta V = (3-0.01V)\Delta t\end{displaymath}

The differential equation is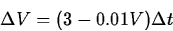

\begin{displaymath} \frac{dV}{dt} = 3 - 0.01V\end{displaymath}

Including the initial value, the model is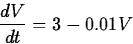

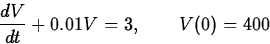
\begin{displaymath} \frac{dV}{dt} + 0.01V = 3,\qquad V(0) = 400\end{displaymath}

c.
What is the physical meaning of the free and forced response of this model?

The free response solves

V' + 0.01V = 0; V(0) = 400

It is the amount of water there would be if you started with 400 liters, added none, and allowed the water to leak out as before.

The forced response solves

V' + 0.01V = 3; V(0) = 400

It is the amount of water there would be if you started with an empty tank, added water as in the original problem, and allowed water to leak out as in the original problem.

4.
(25 points) Consider the differential equation u' = - 2 - u + u2.
a.
Find the equilibria of this differential equation. Solve -2 - u + u2 = 0; the equilibrium are at u = 2 and u=-1

b.
Where are solutions to this equation increasing? Where are they decreasing?

If u>2, then -2-u+u2>0.

If -1<u<2, then -2-u+u2<0.

If u<-1, then -2-u+u2>0.

The solution is increasing if u>2 or u<-1. It is decreasing if -1<u<2.

c.
Decide whether each equilibrium in part (a) is stable or unstable.

The equilibrium at -1 is stable. The equilibrium at 2 is unstable.


Nathan Gibson
1/27/1998