1.
- (a) Just integrate:
-
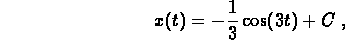
and use the initial data:
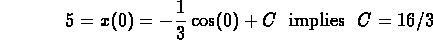
- (b)
-
Separate
integrate and simplify to obtain
Use the initial data to find C:
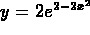
2. You are solving
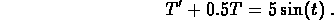
- (a)
-
The corresponding homogeneous equation is
.
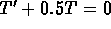The characteristic equation is 
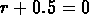, and so 
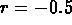and the homogeneous solution is 
.
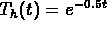- (b)
-
Use the method of Undetermined Coefficients and look for a solution of
the form
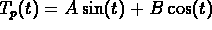. Plug this into the original
equation and equate coefficients to obtain
A = 2 and B = -4.
- (c)
-
The general solution is
.
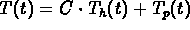The initial condition gives you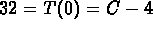 
and
so C = 36.
- (d)
-
The answer is yes: simply choose
.
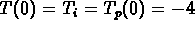(You just have to make the initial data match the initial
value for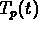 
.)
3. Let
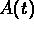denote the amountof carbon monoxide
in the lecture hall at time t (in cubic meters)
and let 
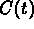denote the concentrationof
carbon monoxide in the hall at time t
(in cubic meters per cubic meter).
Then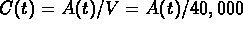 
.
- (a)
-
CO enters the hall at rate
(
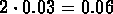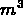/minute).
- (b)
-
CO leaves the hall at the rate
(
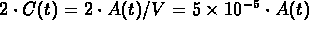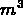/minute).
- (c)
-
The balance equation is
Net change in the amount between t and
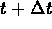= (rate in)
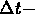(rate out) 
,
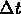or
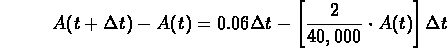
- (d)
-
Collect terms, divide by
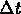and take the limit as
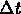approaches zero to obtain the model:
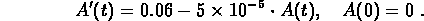
To turn this into an equation for the concentration, replace
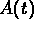by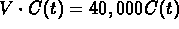 
everywhere that you see it.
4. Sketch the graph of
.
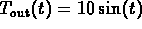The differential equation tells you
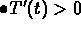when (or where)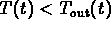 
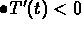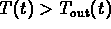
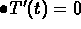when 
when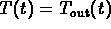 
The last condition tells you that the inside temperature
can have a max or a min only when the the solution curve
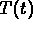crosses the graph of 
.
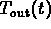It also tells you that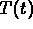 
cannot follow 
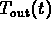exactly (because 
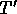would have to be zero everywhere along the
solution).
For the initial data given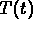 
starts at 0 and stays
strictly below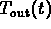 
until the curves cross
(at some time after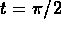
when 
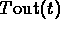is strictly less than 10). This shows that
the amplitude of th inside temperature is smaller than
the amplitude of the outside temperature.