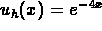and a particular
solution is 
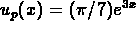. (The method of undetermined
coefficients is perhaps the simplest way to find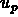 
here.)
The general solution is 
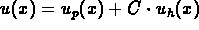where
C is an arbitrary constant.
(b) If you divide by x to put the equation in "standard" form,
you find the integrating factor is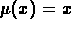 
. So the original
equation is really
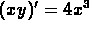and you just integrate to find the general solution
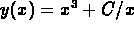, where C is an arbitrary constant.
.
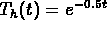(Use the characteristic equation.)
(b) Use the method of undetermined coefficients to obtain
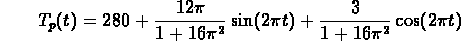
(c) The general solution is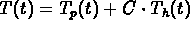 
where C is an arbitrary constant. The initial data gives
you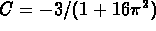 
.
(d) There is no steady state solution (i.e. no constant solution). The exponential part of the solution is transient. The remaining part of the general solution is the limiting periodic solution.
grams.
So the change in this amount would be
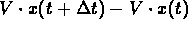grams.
(b)
No TCE is flowing into the lake, so the rate in is zero.
The rate at which TCE flows out of the lake is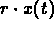 
grams per day.
(c) The balance law gives you
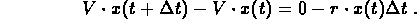
Divide by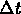 
and take the limit as 
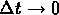to obtain the model:
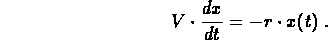
(d) If the rate of inflow is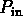 
instead of zero, the
model becomes
.
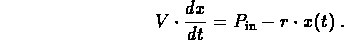
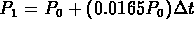Take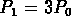 
and solve this equation for 
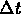to
obtain the approximate tripling time
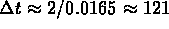years.
© 1996 by Will Brother. All rights Reserved. File last modified on March 22, 1996.
