MA2051 - Ordinary Differential Equations
Old Exam II
Instructions: Do your work on the paper provided. Put your
name and section number on the cover and on each page.
Remember, your work and explanations are graded, not just the
final answer.
1. (35 points) In solving the following problems,
be sure to use work from previous parts if you can.
As always, you must justify your answers.
- (a)
-
Find two linearly independent solutions
for
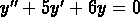 .
Prove that your solutions really are linearly independent.
.
Prove that your solutions really are linearly independent.
- (b)
-
Find a particular solution for
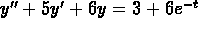 .
.
- (c)
-
Find the solution for
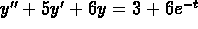 which satisfies
which satisfies 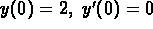 .
.
- (d)
-
For the solution obtained in part (c), describe the behavior
for large values of t.
2. (35 points)
The basic model for an unforced spring is
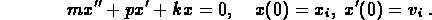
When a mass of 0.2 kilograms is suspended from a spring, it
stretches 0.05 meters.
- (a)
-
Assume for the moment that friction damping can be ignored, so p=0.
Pull the 0.2 kg mass down 15 cm (below equilibrium) and release it from rest.
Write down the corresponding initial value problem and solve
it to find the position of the mass as a function of time.
- (b)
-
Find the period and the amplitude of the motion.
How many times does the mass pass through the equilibrium position
in the first 60 seconds?
- (c)
-
As you observe the motion of the mass, you find that
the amplitude is decreasing;
this tells you that friction damping cannot be ignored.
Explain how to estimate the damping coefficient p
if the amplitude decreases
to 75% of its initial value after the first 60 seconds.
3. (30 points)
Consider the following initial value problem:
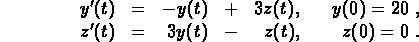
- (a)
-
Give the characteristic equation and find its roots.
Find two linearly independent solution pairs and use them to
obtain the general solution for the system.
- (b)
-
Find the solution satisfying the given initial conditions.
Sketch the graph of the solution curve in the
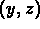 plane.
plane.
- (c)
-
Is it possible to find initial conditions (different than the
given initial conditions) so that the solution
curve converges to the origin
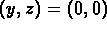 in the
in the 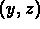 --plane?
Justify your answer.
--plane?
Justify your answer.
© 1996 by Will Brother.
All rights Reserved. File last modified on April 25, 1996.
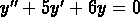 .
Prove that your solutions really are linearly independent.
.
Prove that your solutions really are linearly independent.
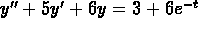 .
.
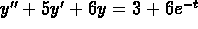 which satisfies
which satisfies 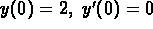 .
.
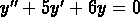 .
Prove that your solutions really are linearly independent.
.
Prove that your solutions really are linearly independent.
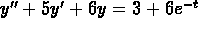 .
.
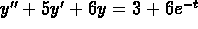 which satisfies
which satisfies 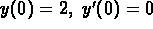 .
.
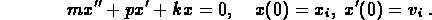
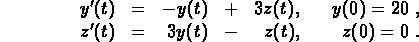
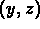 plane.
plane.
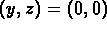 in the
in the 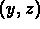 --plane?
Justify your answer.
--plane?
Justify your answer.