MA2051 - Ordinary Differential Equations
Solving ODE's in Maple 






This file gives a very basic introduction to Maple for analyzing ordinary differential equations.


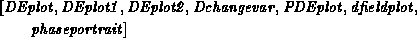
The first thing that you need to do is to open the DE toolbox.


 > with(DEtools); 





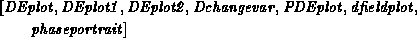
It is easy to get graphs of solution curves.  This first example is a simple (first-order, linear, 
nonhomogeneous) equation:


 > eq:= diff(y(t),t) = sin(t)- 1/2*y(t); 






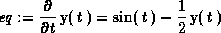
The DEplot command can generate solution curves for you.



> DEplot(eq,[t,y],t=0..12,{[0,0]},y=-3..3,title=`Figure0`);




The solution curve starts out at the point (0,0).   Notice also that it is a little jagged.  This can be 
smoothed out by forcing Maple to use more points in the solution (the default is 20).  You can do 
this by specifying the stepsize:


 >
DEplot(eq,[t,y],t=0..12,{[0,0]},y=-3..3,stepsize=0.1,title=`Figure0:
Smoother`); 


You can put several solutions on the same graph by specifying several initial points.


 > init:= seq([0,i],i=-3..3); 










>
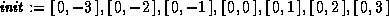
DEplot(eq,[t,y],t=0..12,{init},stepsize=0.2,y=-3..3,title=`Figure1`);



All of the solution curves,  no matter what the initial position, seem to approach one single sine 
curve.




You can get a better feel for the geometry behind the ODE by looking at a direction field.  DEplot 
will produce this if you tell it to add arrows:



>DEplot(eq,[t,y],t=0..12,y=-3..3,arrows=THIN,title=`Figure2: A
Direction Field`);





You can get solutions on top of the direction field if you want to.



>DEplot(eq,[t,y],t=0..12,{[0,0]},stepsize=0.2,y=-3..3,arrows=THIN,
title=`Figure 3`);






Finally, you can also get formulas for the solution with the dsolve command.



> dsolve(eq,y(t));








This does show you what happens for "large" values of t and helps to explain the graph in Figure 1: 
 The exponential term goes to zero.  The influence of the initial condition (which determines the 
value for the constant C1) goes away, and all solutions converge to specific combination of sine 
and cosine.


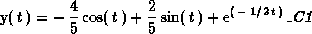
Warning:   There are not many ODEs that have simple formulae for their solutions.  This 
example was linear, so there is a nice solution formula.  If you try to use dsolve on more 
complicated problems, especially noninear problems,  Maple may give no answer, a really strange 
formula,  or lock up your work station.   (Remember the first rule of Maple:  Save Early, Save 
Often!)    Use dsolve with caution.




Here is one more example; just for fun.  This one is a second-order equation.



 > eq2:= diff(y(t),t$2) + w^2*y(t) = sin(w*t);













> dsolve(eq2,y(t));









  

    

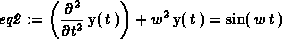
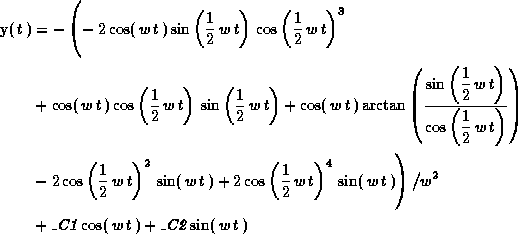
© 1996 by Will Brother.
All rights Reserved. File last modified on October 1, 1996.