MA2051 - Ordinary Differential Equations
D96 Project #2A - Nonlinear Shocks
You have seen in lecture and exercises how to model a
spring-mass system with damping and external forcing.
One application for the model is an
automobile suspension system, where the forcing term is the road
(with or without frost heaves) and shock absorbers provide
the damping.
In this project, you will study the behavior of the solution with
different types of damping terms. Recognize that once you allow the damping
coefficient to depend on the solution, the equation is no longer linear
and most analytic solution methods (such as characteristic equations
and undetermined coefficients) are useless. You have no choice but to
study the system through numerical methods.
- To start, describe the limiting behavior of the standard model
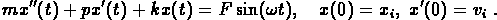
How does the amplitude of the limiting solution depend on 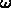 ?
How does it depend on the initial data?
?
How does it depend on the initial data?
Compare your results with the graphs on page 280 and the
formula given in Exercise 12 on page 282 in the text.
-
One of the best ways to analyze the solution curves for
a second-order equation is to
graph them in the
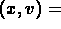 (position, velocity) plane.
Derive a system of first-order differential equations for
(position, velocity) plane.
Derive a system of first-order differential equations for
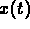 and
and 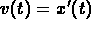 and plot solution curves in the
and plot solution curves in the
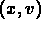 plane. Pay particular attention to the limiting behavior
of the solutions. How does the limit depend on the initial data?
How does it depend on other parameters in the model?
plane. Pay particular attention to the limiting behavior
of the solutions. How does the limit depend on the initial data?
How does it depend on other parameters in the model?
-
Mathematicians and engineers at the Renault Automobile Company
have studied a new type of shock absorber which controls the
damping coefficient. Their new shock absorber can increase the
damping coefficient whenever the mass (i.e., the car) is returning
toward equilibrium. In the mathematical
model, the damping coefficient is a discontinuous function of
both
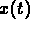 and
and 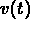 .
.
Do some numerical experiments with the Renault shock absorber.
Explain in detail how you program the damping coefficient in your equation.
Take 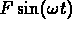 for the forcing function and
describe the limiting behavior of the solution for a range of
for the forcing function and
describe the limiting behavior of the solution for a range of 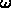 values.
Does the new shock absorber give a "smoother" ride than the
original shock absorber? Do
you think that Renault should pursue its development of this new shock
absorber?
values.
Does the new shock absorber give a "smoother" ride than the
original shock absorber? Do
you think that Renault should pursue its development of this new shock
absorber?
-
Design your own shock absorber and analyze the resulting
system of differential equations. Can yo do better then
Renault?

© 1996 by Will Brother.
All rights Reserved. File last modified on April 25, 1996.
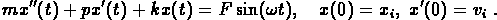
 ?
How does it depend on the initial data?
?
How does it depend on the initial data?
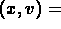 (position, velocity) plane.
Derive a system of first-order differential equations for
(position, velocity) plane.
Derive a system of first-order differential equations for
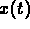 and
and 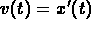 and plot solution curves in the
and plot solution curves in the
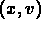 plane. Pay particular attention to the limiting behavior
of the solutions. How does the limit depend on the initial data?
How does it depend on other parameters in the model?
plane. Pay particular attention to the limiting behavior
of the solutions. How does the limit depend on the initial data?
How does it depend on other parameters in the model?
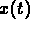 and
and 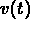 .
.
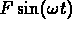 for the forcing function and
describe the limiting behavior of the solution for a range of
for the forcing function and
describe the limiting behavior of the solution for a range of 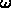 values.
Does the new shock absorber give a "smoother" ride than the
original shock absorber? Do
you think that Renault should pursue its development of this new shock
absorber?
values.
Does the new shock absorber give a "smoother" ride than the
original shock absorber? Do
you think that Renault should pursue its development of this new shock
absorber?
