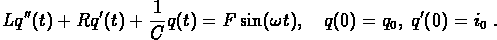
MA2051 - Ordinary Differential Equations
D96 Project #2B - Nonlinear Resistance 




   You have seen in lecture and exercises how to model a forced 
spring-mass system with damping.   The mathematical model
for the charge on the capacitor in an LRC circuit is exactly the same:







    

  1.   To start, do some numerical experiments with this basic model. 
Focus on the limiting behavior of the solution. 
How does the amplitude of the limiting solution depend on ?
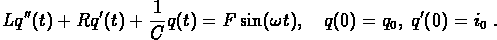
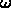How does it depend on the initial data?

    
Compare your results with the graphs on pages 286 and 287 in your text.

    

    

  2. 
Second-order differential equations can be rewritten
as systems of first-order equations.  Take F=0 (so there
is no source term)  and verify that the differential
equation given above can be rewritten as 


    

    

Plot some solution curves for this model in the 
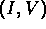 plane.   
For simplicity (and sanity), choose parameter values C=1 and
L=1. 
How do the solutions change with R?

    

     

  3. 
It is possible to design a circuit that will produce a periodic 
output current even when there is no source term. 
Circuits such as these were developed for the first commercial
radios in the 1920's. 
Balthazar van der Pol designed a circuit in which the
passive resistor is replaced by an active element
which would pump energy into the circuit whenever the amplitude
of the current falls below a certain level. 
(In the 1920's, these active elements were vacuum tubes.)
In the van der Pol circuit, the potential drop across the
active element (which used to be just RI) is given by a
nonlinear function such as .

    
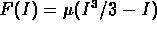Do some numerical studies of the van der Pol circuit.  
For simplicity, take C=1 and L=1 as in the last part. 
Focus on how the solution changes for different values of the
parameter .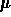

    
The resulting limit cycles are sometimes called relaxation
oscillations. Can you explain this terminology?  (You may want
to visit your favorite, and most relaxed, electrical engineer.)

    

    

  4.  
Design your own active element.  Specify a functional form
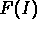for  and compare the behavior of your circuit with
van der Pol's.

    






  

    

      © 1996 by Will Brother.
      All rights Reserved. File last modified on April 25, 1996.