MA2051 - Ordinary Differential Equations
Project #1
You can make a lot of money harvesting from a population
that grows exponentially. The trouble is that almost no
population in the real world can exhibit exponential
growth (for very long).
In this project, you will look at harvesting for populations
that exhibit realistic, logistic growth.
-
Start with paper and pencil and investigate the solution curves
for the logistic growth model (without harvesting).
The basic model is
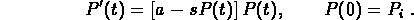
Use some basic calculus to sketch solution curves (for several
different initial values 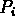 ).
For what values of P is the solution increasing? decreasing?
concave up? concave down?
Work directly from the model; you do not need a formula for
the solution to do this analysis.
).
For what values of P is the solution increasing? decreasing?
concave up? concave down?
Work directly from the model; you do not need a formula for
the solution to do this analysis.
-
Now go to the computer lab and
use your favorite software package to graph some solution curves.
Choose values for the parameters (a and s)
so that the population would settle down at
a final value of 100 (if you wait long enough).
Compare the computer output with your qualitative analysis
from part (1).
-
Now start harvesting. Work with constant harvest rates.
Is there a maximum, sustainable (constant) harvest rate?
How does the maximum harvest rate depend on the parameters
a and s?
Is there a harvest rate that will wipe out the population,
no matter how large you make
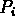 ?
Use your favorite software package to graph solution curves
for several different examples to illustrate your conclusions.
?
Use your favorite software package to graph solution curves
for several different examples to illustrate your conclusions.
-
Explore some nonconstant harvest policies. (Get creative.)
Compare your different policies in terms of their yield.
(Be sure to define yield along the way.)
Can you do better than the constant policies studied in
part (3)?
 First Draft Due: Thursday, March 28, 1996
First Draft Due: Thursday, March 28, 1996
 Final Draft Due: Tuesday, April 2, 1996
Final Draft Due: Tuesday, April 2, 1996

© 1996 by Will Brother.
All rights Reserved. File last modified on March 22, 1996.
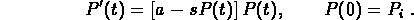
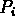 ).
For what values of P is the solution increasing? decreasing?
concave up? concave down?
Work directly from the model; you do not need a formula for
the solution to do this analysis.
).
For what values of P is the solution increasing? decreasing?
concave up? concave down?
Work directly from the model; you do not need a formula for
the solution to do this analysis.
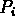 ?
Use your favorite software package to graph solution curves
for several different examples to illustrate your conclusions.
?
Use your favorite software package to graph solution curves
for several different examples to illustrate your conclusions.
 First Draft Due: Thursday, March 28, 1996
First Draft Due: Thursday, March 28, 1996
 Final Draft Due: Tuesday, April 2, 1996
Final Draft Due: Tuesday, April 2, 1996
