- (a)
- Just integrate to obtain
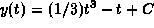 and use the
initial data to find C = 3.
and use the
initial data to find C = 3.
- (b)
- Separate and integrate (using partial fractions) to
obtain
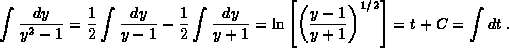
Rearrange to find

and use the initial data to find
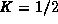 .
Solve finally for y,
.
Solve finally for y,

and note that this solution is valid only for
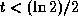 if
you start at t = 0.
if
you start at t = 0.
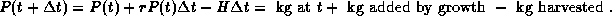
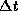 and let
and let 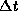 go to zero to obtain
go to zero to obtain

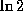 divided by the doubling time, so
divided by the doubling time, so 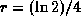 .
.
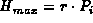 where
where 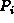 is the initial population.
You can get this from the solution for the initial value problem or
just by setting the righthand side of the differential
equation equal to zero. You have
is the initial population.
You can get this from the solution for the initial value problem or
just by setting the righthand side of the differential
equation equal to zero. You have 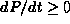 , so the
population does not decay, if and only
if
, so the
population does not decay, if and only
if 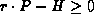 . If, on the other hand,
. If, on the other hand,
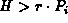 , then
, then 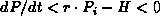 for
all time and the yeast population will reach zero.
The amount harvested in a day with
for
all time and the yeast population will reach zero.
The amount harvested in a day with 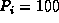 kg and
kg and 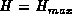 is then
is then 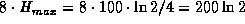 , which is approximately
, which is approximately 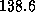 kg per day.
kg per day.
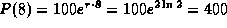 kg per day,
which is a much larger yield per day than the maximum for
constant harvesting.
kg per day,
which is a much larger yield per day than the maximum for
constant harvesting.
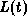 is a homogeneous solution and
is a homogeneous solution and 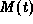 is a particular
solution so, because the equation is linear, the general solution
is
is a particular
solution so, because the equation is linear, the general solution
is 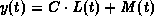 . The initial data determine C
from
. The initial data determine C
from 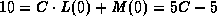 , or C= 3.
, or C= 3.
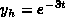 .
.
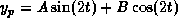 . Plug it in to obtain
the equations 2A + 3B = 13 and 3A - 2B = 0 for A and B.
The solutions are A=2 and B=3.
. Plug it in to obtain
the equations 2A + 3B = 13 and 3A - 2B = 0 for A and B.
The solutions are A=2 and B=3.
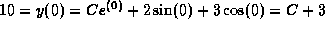 and obtain C= 7, hence
and obtain C= 7, hence
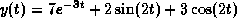 .
.
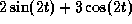 for large t.
for large t.
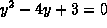 to obtain two steady states
y=1 and y=3; these are constant solutions for the differential
equation.
to obtain two steady states
y=1 and y=3; these are constant solutions for the differential
equation.
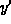 is positive and so y is increasing for y<1
and y > 3.
is positive and so y is increasing for y<1
and y > 3. 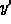 is negative and so y is decreasing
for 1 < y < 3.
The solution starting at 0 increases and approaches y=1.
The solution starting at 1 remains y=1.
The solution starting at 5 increases and does not approach anything.
is negative and so y is decreasing
for 1 < y < 3.
The solution starting at 0 increases and approaches y=1.
The solution starting at 1 remains y=1.
The solution starting at 5 increases and does not approach anything.
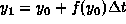 with
with 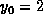 ,
,
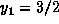 and
and 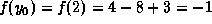 . You obtain
. You obtain
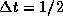 (whatever units you want).
(whatever units you want).