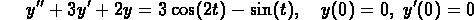MA2051 - Ordinary Differential Equations
Review For Test II
1.
Work with the following differential equation:
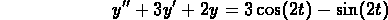
-
(a)
-
Find two linearly independent solutions for the
corresponding homogeneous equation.
Prove that your solutions really are linearly independent.
-
(b)
-
Find a particular solutionfor the original equation.
-
(c)
-
Find the solution for the equation which satisfies
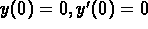 .
.
-
(d)
-
Does the solution have a transient component?
If it does, estimate how long it takes for the
magnitude of this component to become less than
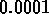 .
.
-
(e)
-
Does the equation have a limiting periodic solution? If it does,
identify the amplitude and period of this limiting solution.
-
(f)
-
Determine initial values (
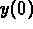 and
and 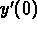 ) so that the
solution to the initial value problem contains no transient
component.
) so that the
solution to the initial value problem contains no transient
component.
2. Consider the two functions
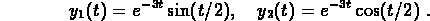
-
(a)
-
Find a linear, constant-coefficient, homogeneous
differential equation that has
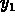 and
and 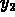 as solutions.
as solutions.
-
(b)
-
Determine initial conditions
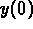 and
and 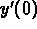 so that
so that 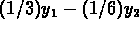 is the solution for the differential
equation that you found in (a).
is the solution for the differential
equation that you found in (a).
3.
A mass of 6 kg is suspended from a spring that extended 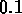 m
when a 1 kg mass was attached. Assume that friction damping
can be ignored (until part (d)). You pull the mass
down5 cm and release it from rest.
m
when a 1 kg mass was attached. Assume that friction damping
can be ignored (until part (d)). You pull the mass
down5 cm and release it from rest.
-
(a)
-
Write down the mathematical model for this
system. Use the given data to
specify the numerical values for the parameters in the model.
-
(b)
-
Determine the natural frequency,the
period,and the amplitude
of the motion of the mass.
-
(c)
-
How much would you have to increase the mass in order to
double the period? How much would you have to
increase the mass in order to double the the amplitude?
-
(d)
-
Take the same spring-mass system and immerse it
in a vat of molasses. It is no longer reasonable to
ignore the force of friction damping.
For what values of the
damping coefficient p will the spring still exhibit
oscillations about the steady state? Explain your answer.
4. Consider the following system of first-order
differential equations:

-
(a)
-
Find two solution pairs and verify that they are linearly independent.
Give the general solution for the system.
-
(b)
-
Find the solution satisfying initial conditions
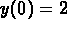 and
and 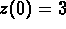 .
.
-
(c)
-
Graph the solution obtained in part (b) in the
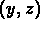 --plane, you would find that it is a spiral going
out away from the origin.
--plane, you would find that it is a spiral going
out away from the origin.
-
(d)
-
Using only the differential equation (and not the actual solution),
show that the quantity
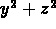 is actually increasing
along any solution curve and so the solution must be heading
away from the origin.
is actually increasing
along any solution curve and so the solution must be heading
away from the origin.
5.
Use two steps of Euler's method to approximate the solution to
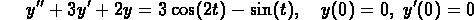
at t = 1. Compare your numerical result with the exact solution
obtained in problem #1 above. What is the error?
© 1996 by Will Brother.
All rights Reserved. File last modified on April 25, 1996.
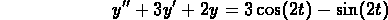
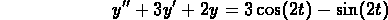
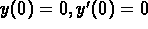 .
.
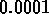 .
.
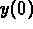 and
and 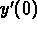 ) so that the
solution to the initial value problem contains no transient
component.
) so that the
solution to the initial value problem contains no transient
component.
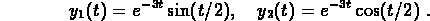
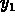 and
and 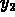 as solutions.
as solutions.
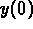 and
and 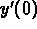 so that
so that 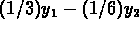 is the solution for the differential
equation that you found in (a).
is the solution for the differential
equation that you found in (a).
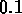 m
when a 1 kg mass was attached. Assume that friction damping
can be ignored (until part (d)). You pull the mass
down5 cm and release it from rest.
m
when a 1 kg mass was attached. Assume that friction damping
can be ignored (until part (d)). You pull the mass
down5 cm and release it from rest.

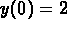 and
and 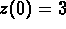 .
.
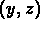 --plane, you would find that it is a spiral going
out away from the origin.
--plane, you would find that it is a spiral going
out away from the origin.
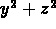 is actually increasing
along any solution curve and so the solution must be heading
away from the origin.
is actually increasing
along any solution curve and so the solution must be heading
away from the origin.