MA 2051 D '97 Sample Exam 1

Show your work in the space provided. Unsupported answers may not receive full credit.

1. Explain what it means for a function u to be a solution of the DE y' = f(x,y) on an interval .
2. Consider the following differential equation.

   

   1. Use the method of characteristics to find the general solution of the corresponding homogeneous equation.
   2. Find a particular solution, using the method of undetermined coefficients.
   3. Find a solution that satisfies the initial condition y(-1)=5.
3. Consider the differential equation

   

   1. Is this DE linear? Explain why or why not.
   2. Use separation of variables to solve the corresponding homogeneous differential equation. For which values of x does your solution make sense?
   3. Use variation of parameters to find the general solution to the differential equation.
   4. Can you find a solution that satisfies the initial condition y(0)=2? If your answer is yes, give your solution. If your answer is no, explain what goes wrong.
4. Imagine that you were trapped at home during the recent blizzard. Unfortunately, you were unlucky enough to lose power. You are well-prepared, however, with a supply of candles and fuel for your wood stove.
   1. Derive a model to describe the temperature in your house, assuming the temperature outside is constant at 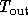and that the stove generates heat at a constant rate Q in units of energy per unit time.
   2. Solve the differential equation you derived above for the initial condition .
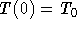   3. Explain the qualitative behavior of your model.

• About this document ...