MA 2051 D '97 Sample Exam 1

Show your work in the space provided. Unsupported answers may not receive full credit.

1. Explain what it means for a function u to be a solution of the DE y' = f(x,y) on an interval .

   The function u is a solution if it is continuously differentiable on the interval and satisfies

   

2. Consider the following differential equation.

   

   1. Use the method of characteristics to find the general solution of the corresponding homogeneous equation.

      The characteristic equation is r+2 = 0, so the general solution to the homogeneous equation is

      

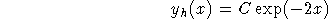
   2. Find a particular solution, using the method of undetermined coefficients.

      The form for 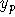is

      

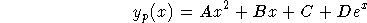
      This gives

      

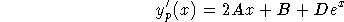
      so we have

      

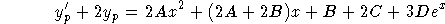
      Comparing to the right-hand side of our DE, we get the equations

      

      The solution is A=1/2, B=-1/2, C=1/4, and D=1 so

      

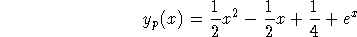
   3. Find a solution that satisfies the initial condition y(-1)=5.

      The general solution is 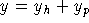. Evaluating at y=-1 gives

      

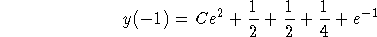
      so we have

      

3. Consider the differential equation

   

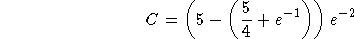
   1. Is this DE linear? Explain why or why not.

      This DE is linear. If 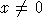we can write it in our standard form

      

      as

      

   2. Use separation of variables to solve the corresponding homogeneous differential equation. For which values of x does your solution make sense?

      Separation of variables gives

      

      Integrating, and making the usual argument gives the solution

      

      as long as .

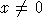   3. Use variation of parameters to find the general solution to the differential equation.

      To use VOP, we write 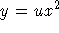and substitute into the left-hand side of the DE.

      

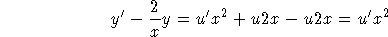
      Setting this equal to the right-hand side and solving for u', we get

      

      which gives

      

      Multiplying by gives the general solution as

      

   4. Can you find a solution that satisfies the initial condition y(0)=2? If your answer is yes, give your solution. If your answer is no, explain what goes wrong.

      Simply plugging x=0 into our general solution gives y(0) = 0, so there is no way to match the initial condition. What goes wrong is that the coefficient 1/x is undefined at x=0, so we can't expect to get a solution at x=0.

4. Imagine that you were trapped at home during the recent blizzard. Unfortunately, you were unlucky enough to lose power. You are well-prepared, however, with a supply of candles and fuel for your wood stove.
   1. Derive a model to describe the temperature in your house, assuming the temperature outside is constant at 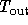and that the stove generates heat at a constant rate Q in units of energy per unit time.

      Using the same letters to denote parameters that we used in class, we get

      

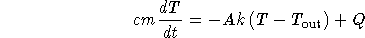
      for the energy balance equation. Dividing both sides by cm gives

      

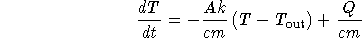
   2. Solve the differential equation you derived above for the initial condition .

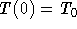      One way to solve this IVP is to write the DE in standard linear form as

      

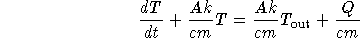
      The homogeneous solution can easily be obtained using the characteristic equation as

      

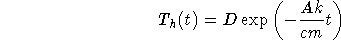
      and the particular solution can be obtained using the method of undetermined coefficients as

      

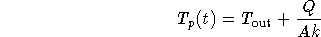
      Combining the particular and homogeneous solutions and applying the initial condition, we get the following solution.

      

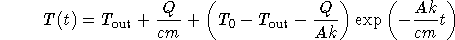
   3. Explain the qualitative behavior of your model.

      The solutions of this model decay exponentially to the constant

      

      Note that this is greater than 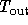, because of the heat source Q.

• About this document ...