MA 2051 D '97 Sample Exam 2

1. Consider the following differential equation, describing a damped spring-mass system.

   

   1. Find the roots of the characteristic equation. Classify the spring-mass system as underdamped, overdamped, or critically damped.
   2. Find two linearly independent solutions to the differential equation. Use the Wronskian to prove that your solutions really are linearly independent.
   3. Find the solution that satisfies the initial conditions x(0)=-2, x'(0) = 4.
2. Consider the forced, undamped spring-mass differential equation shown below.

   

   1. Find the general solution of the homogeneous differential equation.
   2. Find a particular solution.
   3. Find the general solution that satisfies the initial conditions x(0)=1 and x'(0)=-2.
3. Consider the following system of differential equations.

   

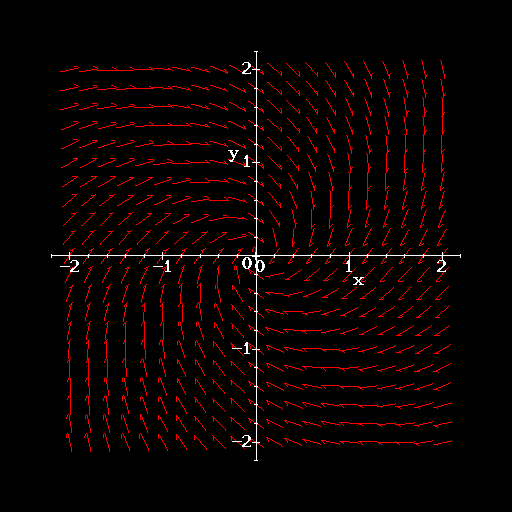
   1. Find the characteristic equation and determine its roots.
   2. Find the two linearly independent solutions. (You need not verify that they are linearly independent.)
   3. Find the solution that satisifies the initial condition x(0)=0, y(0)=5.
   4. Sketch the phase portrait for this system over the region 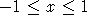, 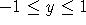. Include at least four trajectories in your sketch.
4. On the direction field given below, sketch trajectories starting at the initial conditions x(0)=-1, y(0)=0.5 and x=1.5, y(0)=0.