MA 2051 D '97 Sample Exam 2

1. Consider the following differential equation, describing a damped spring-mass system.

   

   1. Find the roots of the characteristic equation. Classify the spring-mass system as underdamped, overdamped, or critically damped.

      The characteristic equation is

      

      The roots are complex, .

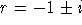   2. Find two linearly independent solutions to the differential equation. Use the Wronskian to prove that your solutions really are linearly independent. The two solutions are

      

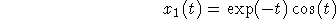
      and

      

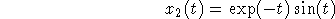
      The Wronskian is given by the determinant

      

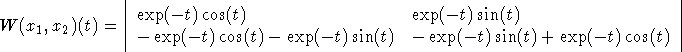
      After simplification, and using the trig identity 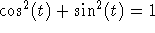, we get

      

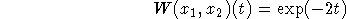
   3. Find the solution that satisfies the initial conditions x(0)=-2, x'(0) = 4. The general solution is

      

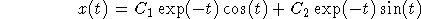
      and the derivative is

      

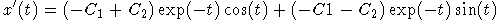
      So plugging in t=0 gives the two equations

      

      Solving gives , .

2. Consider the forced, undamped spring-mass differential equation shown below.

   

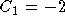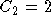   1. Find the general solution of the homogeneous differential equation.

      The general solution to the homogeneous equation is

      

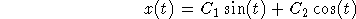
   2. Find a particular solution. The forcing term is a solution to the homogeneous equation, so the particular solution must have the form

      

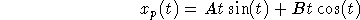
      This gives

      

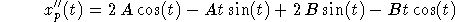
      so

      

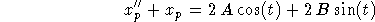
      Comparing to the forcing term, we get A=1, B=0, so

      

   3. Find the general solution that satisfies the initial conditions x(0)=1 and x'(0)=-2.

      The general solution is

      

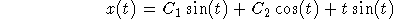
      The derivative is

      

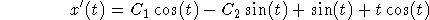
      so the equations to be satisfied are

      

3. Consider the following system of differential equations.

   

   1. Find the characteristic equation and determine its roots.

      The characteristic equation is

      

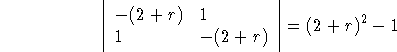
      So the roots are r=-1 and r=-3.

   2. Find the two linearly independent solutions. (You need not verify that they are linearly independent.)

      For r=-3, the equation is A + B =0 so a good choice is A=1, B=-1. For r=-1, the equation is -A + B =0 so a good choice is A=1, B=1. So the two linearly independent solutions are

      

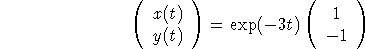
      and

      

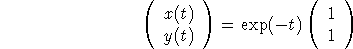
   3. Find the solution that satisifies the initial condition x(0)=0, y(0)=5.

      The equations to be satsified are

      

      so 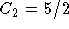and 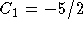. The solution is

      

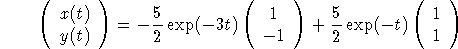
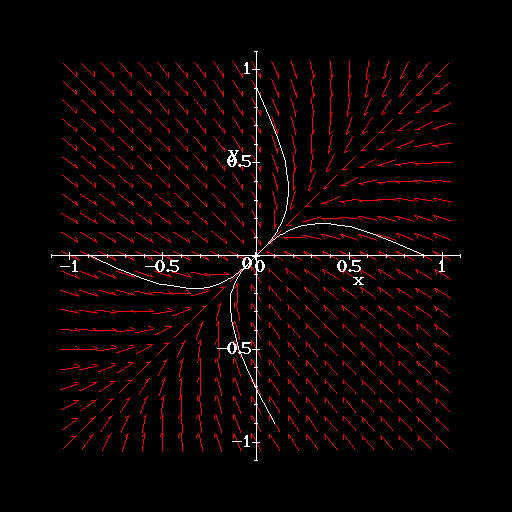
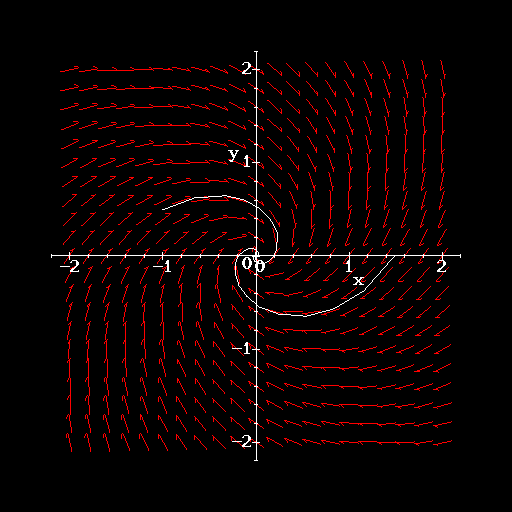
   4. Sketch the phase portrait for this system over the region 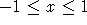, 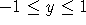. Include at least four trajectories in your sketch.

      

4. On the direction field given below, sketch trajectories starting at the initial conditions x(0)=-1, y(0)=0.5 and x=1.5, y(0)=0.