The basic Maple command for solving differential equations is dsolve. This command can be used to obtain analytical solutions of linear equations as well as numerical solutions of nonlinear equations. The basic syntax of the dsolve command for a single linear equation is
> dsolve(deq, initcond,func);
where deq represents a differential equation, initcond stands for one or more initial conditions, and func is the function representing the solution of the differential equation.
Several other Maple commands will be useful to us, including the diff command for computing derivatives, the subs command for substituting sets of parameter values into differential equations and their soloutions, and several commands from the DEtools package for plotting slope fields and phase portraits.
This document provides examples of for all of these commands. It begins with examples of solving linear first and second order differential equations and then goes on to describe the plotting commands from the DEtools package.
Consider the following differential equation.
The solution, obtained by separation of variables (or otherwise) is
where C is a constant. The Maple command to solve this differential equation is given below, as well as the output.
> dsolve(diff(x(t),t) = -k*x(t) ,x(t));
The first thing to notice is that the Maple command needs you to specify explicitly in a couple of places that x depends on t. We don't always do this when writing down differential equations by hand, but Maple often needs more guidance.
Actually Maple isn't quite that stupid, because the following shortcut does work.
> dsolve(diff(x(t),t) = -k*x ,x(t));
However, if you replace either of the remaining occurrences of x(t) with x you will get an error. To avoid problems, I would stick with using x(t) all the time. You can never go wrong by underestimating the intelligence of Maple!
Another thing to notice is that Maple uses 
to stand for the
constant C. Putting the underscore in front is just Maple's way of
minimizing the risk of a conflict with a variable you have set. You
might try to see what Maple does if you give the variable
_C1 a value.
The final thing to notice is that the output of the dsolve command is an equation, with the expression for the solution appearing on the right-hand side of the equation. If you need this expression for plotting or further manipulation, you will have to somehow extract it from the equation. If you are using dsolve to solve a single differential equation, then using the rhs command is the easiest way to accomplish this.
To use the rhs command, you have to be able to access the output of the dsolve command. The best way to do this is to give the dsolve command a label, as in the following example. It usually makes sense to also provide a label for the expression you've extracted, so it will be easy to plot it, differentiate it, or otherwise use it.
> sol1 := dsolve(diff(x(t),t) = -k*x(t) ,x(t));
> x1 := rhs(sol1);
You can also specify initial conditions in the dsolve command. For example, we could solve the IVP
with the following command.
> sol2 := dsolve({diff(x(t),t) = -k*x(t),x(0) = 120},x(t));
Note that you have to put the differential equation and the initial condition together and enclose them in curly braces ({}).
The simple example we have been using includes a parameter k. Before we can plot the solution we have to set its value. If you are going to set one value for k and not change it, then you can just use a command like the first one below. The other command just shows that the value of k has been set.
> k := 1/4;
> x1;
However, sometimes you want to give a parameter several values, perhaps to plot the solution for different parameter values or because you need the general form of the solution for something else. In these cases, setting the values of parameters is best done with the subs command, as shown below. (The first command just unsets the value of k so it is treated as a variable again.)
> k := 'k';
> subs(k=1/4,x1);
The final example in this section demonstrates how to plot the solution to the IVP
which we labeled above with the name sol2. For the plot command to work, Maple has to be able to evaluate the expresssion being plotted to a number. This means that the value of k has to be set. The command below shows how to use the subs command to do this.
> plot(subs(k=1/4,rhs(sol2)),t=0..5);
For this section we consider the following second order differential equation with constant coefficents
where m, c and k are constants. The procedure for using Maple to solve this second order equation is very similar to what we did in the previous section, but there are two main differences.
To proceed, we first define our differential equation and give it a label. This will save some typing later on.
> de1 := m*diff(x(t),t,t)+c*diff(x(t),t) + k*x(t) = 0;
Next, we define a set of values for our parameters.
> par1 := {m=1, c= 1/10, k=4};
Finally, we substitute the parameter values and solve the IVP
with the command
> sol3 := dsolve(subs(par1,{de1,D(x)(0) = 0, x(0) = 1}), x(t));
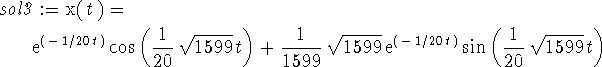
Note how the initial condition for x' is specified. We can extract the solution the same way we did before, with the command
> x3 := rhs(sol3);
This result can now be plotted or otherwise manipulated as desired.
As a final example, note that above we substituted the parameter values in the differential equation and then solved it. You can proceed by first solving and then substituting parameter values, as we did for the first order equation, but substituting and then solving is usually preferable.
To see this, suppose we solve the IVP with new initial conditions x(0) = and x'(0) = 1 without substituting parameter values first, as shown below.
> sol4 := dsolve({de1,D(x)(0) = 1,x(0) = 0},x(t));
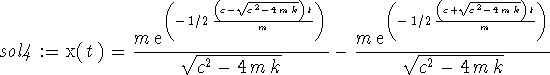
Here is the result of substituting our parameter values.
> subs(par1,sol4);
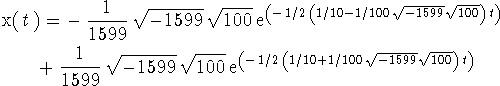
If we do things in the opposite order, the result is simpler, as shown below.
> sol5 := dsolve(subs(par1,{de1,D(x)(0) = 1,x(0) = 0}),x(t));
