Project 1 Computer Networks and Graphs
Introduction: your group has been given the task of reviewing the computer networks of a national manufacturing company. The wide area networks (WANs) are already in place, but questions have been raised concerning reliability and security, as well as cost.
The company you have been hired by manufactures small runs of one of a kind micro electrical components such as miniature motors and pumps. The turnaround time from design to manufacture to shipment is very short and the companies ability to be responsive is a key element in its success.
One element in the responsiveness of the company has been its ability to make use of electronic communication; not just e-mail but images, video, and conference work. This has meant that at a moments notice, the entire expertise of the company may be focused on a problem, regardless of the physical location of the involved parties. Also, computer generated prototypes often involve reworking at the customers sight, with the involvement of engineers in other areas of the country.
Recent breaches in the security of Internet have made the company realize that it may be vulnerable, and communications downtime of any length is not something it can afford.
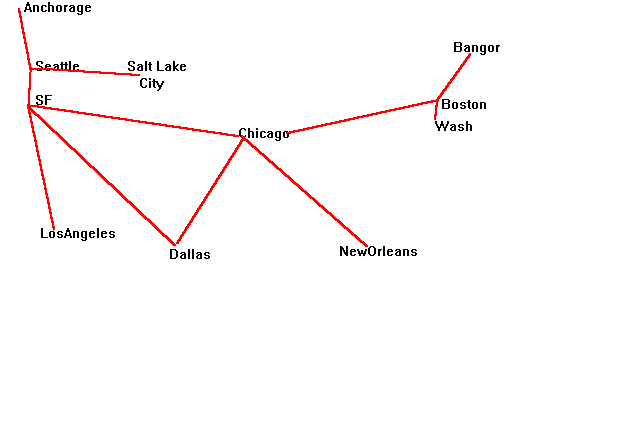
Further Information: the company has property in Seattle, San Francisco, Salt Lake City, New Orleans, Boston, Nashua NH,Anchorage, Dallas, Chicago and Worcester. It also has a subcontractor in Seoul, South Korea which it communicates with via satellite. All other lines are dedicated data lines rented from companies such as AT&T and MCI.
A graph of the communications paths is below; this shows how the major locations are joined. In addition, each location has offices and plants within it and each of those has its own topology.

Background: section 8.1 of Kolman; any book with introductory material on graph theory and adjacency matrices such as Applied Combinatorics by Fred Roberts (1984, Prentice-Hall)
Goals: The overall goal is to develop mathematical techniques and algorithms which might be used by the company in the future to study and evaluate their networks. Thus, while accurate answers to the problems below are important, of even greater importance is the written description of the technique used to obtain it.
In each of parts 2-4 , please provide an answer in two ways:
a. by generating an answer (or answers) by hand or visually, using the sample network provided
b. by developing a matrix based method which would yield the information needed for any communication network, no matter how big. Please describe your method with suitable clarity so someone from the communications company may understand and implement it.
Part 1. set up the "adjacency matrix" for the graph described above.
Part 2. in networking terms, for a given communication from one place to another, a hop is defined as the number of intermediate sites it must go through to get where it is going. For example, if one sends email from Boston to Seattle , then there are 2 hops.
Find the worst cases of communications in terms of numbers of hops involved.
Part 3. In terms of security, we are interested in those situations where there are few or no options for given communication between 2 sites. If there is only one path for a given communication, then that communication is vulnerable should that path break down.
Give all communication paths a "susceptibility index" which equals the number of different ways that a message may get from one site to another. Clearly, then, those pairs with a susceptibility index value of 1 are of great concern. (this should be presented in table form)
Make recommendations as to what links you would add to improve the reliability of the network.
Part 4. the company is also concerned about measuring usage. Specifically, how much information is passing through one site as compared to another.
By examining powers of the adjacency matrix, what can you say about this? Of interest may be the fact that if you multiply a matrix by a column of all 1s, the result is a column of row sums. Similarly if you multiply on the left by a row of all 1s, the result is a row of all column sums. (try it out by hand!)
Part 5. Next, find the largest positive eigenvalue of the adjacency matrix and an eigenvector associated with it. Can you relate the components of the vector in any way to your results about usage? There are two ways this may possibly be done:
a. by the "Power Method" (see project 5 )
b. by using an appropriate software function such eigenvals in Maple
or poly and roots in Matlab.
References Information on networking may be found in Technical Aspects of Data Communication (2nd ed) by John McNamara (Digital Press) as well as many other books.