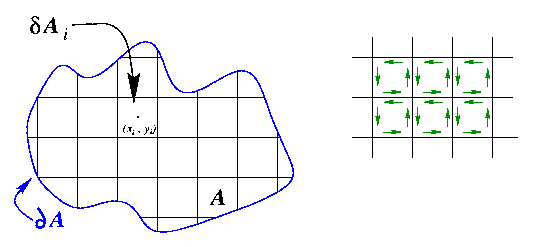
Consider a region
![]() whose boundary
whose boundary
![]() is a rectifiable simple closed curve.
Partition
is a rectifiable simple closed curve.
Partition ![]() into a set of sufficiently small rectangles
into a set of sufficiently small rectangles
![]() (near the boundary, the partition elements are not necessarily rectangular).
Let
(near the boundary, the partition elements are not necessarily rectangular).
Let
![]() denote the area of
denote the area of
![]() .
For each of the
.
For each of the
![]() ,
let
,
let
![]() be a point in the interior of
be a point in the interior of
![]() .
.
From the definition of divergence,
for the point
![]() in the partition element
in the partition element
![]() ,
,
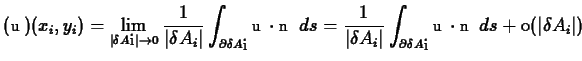
Now, summing over all of the partition elements,
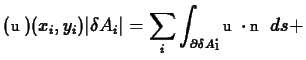 O
O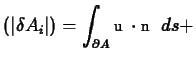 O
O
Finally, taking the limit as
![]() , one finds
, one finds
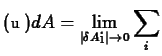 div
div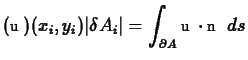
Reference: P.C. Mathews, Vector Calculus, Springer-Verlag, London, 1998.
Copyright, 2001, Joseph D. Fehribach