Histogram in which area, rather than height of bar, represents frequency.
- This allows proper representation of histograms with unequal interval widths.
- For a density histogram the bar height is the density of the bar: the relative frequency/(unit interval length).
- Bernoulli trial
- Probability of success: limit of relative frequencies.
- Random phenomenon
- Trial, Event
- Probability of an event
- Random phenomenon: Toss a pair of dice.
- Events: Lots of possibilities. Consider two:
- A={Roll a 7}
- E={Roll an even number}
- Probability of an event:
-
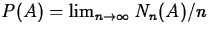 , where Nn(A) is the number of times 7 comes up in n rolls.
, where Nn(A) is the number of times 7 comes up in n rolls.
-
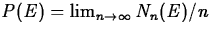 , where Nn(E) is the number of times an even number comes up in n rolls.
, where Nn(E) is the number of times an even number comes up in n rolls.
-
- Random phenomenon: A critical landing gear component on a commercial airliner is inspected once per week and replaced when it exhibits excessive wear.
- Events: Lots of possibilities. Consider two:
- A={Lasts less than three weeks}
- E={Lasts more than a year}
-
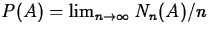 , where Nn(A) is the number of times the part was replaced in
less than three weeks in n replacements.
, where Nn(A) is the number of times the part was replaced in
less than three weeks in n replacements.
-
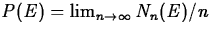 , where Nn(E) is the number of times the part lasted more
than a year in n replacements.
, where Nn(E) is the number of times the part lasted more
than a year in n replacements.
Events are sets of outcomes of a random phenomenon, so we can perform operations on events that we do to sets. Among these are intersections and unions. If two events have no outcomes in common, they are disjoint. Their intersection is the null event.
![]()
![]()
![]()
This follows from the addition rule of probability.
Two events are independent if knowing whether one occurs does not change the probability that the other occurs.
It can be shown that events A and B are independent if and only if the multiplication rule holds:
![]()
We can define the notion of mutual independence of more than two events: see the book, p. 125.
Two trials of a random phenomenon are independent if any event from the first trial is independent of any event from the second trial.
- Discrete random variable
- Discrete distribution model
- Probability mass function
Assume Y is a discrete random variable with probability mass function pY(y).
- Mean
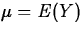 exists if
exists if
In this case,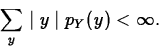
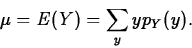
- The variance,
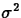 exists if
exists if
In this case,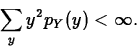
The standard deviation is the square root of the variance.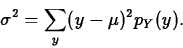
- Probabilities For any set A of real
numbers,
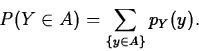
A floor is constructed of square tiles of sides 1, 2 and 4 inches. The numbers of these tiles are in the ratios 24:2:1. You toss a pin on the floor at random. If the tip of the pin lands in a square of side length Y, you win $Y.
- Why is Y a discrete random variable?
- Find the distribution of Y.
- Find the expected value of Y.
- What is a fair admission price to charge someone to play this game?
- Bernoulli
- Description/use:
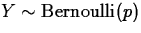 is the
number of successes in one trial with probability p of
success.
is the
number of successes in one trial with probability p of
success.
- Probability mass function:
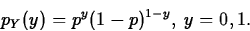
- Mean, variance:
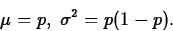
- Description/use:
- Uniform
- Description/use:
 is the value selected ``at random'' from
the integers
is the value selected ``at random'' from
the integers 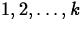 .
. - Probability mass function:
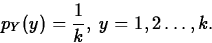
- Mean, variance:
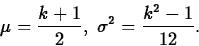
- Description/use:
- The random variable Y refers to the act of taking the measurement. It is random.
- The observed value y refers to the value taken. It is not random.
- Example 1: Roll Them Bones Suppose the random variable Y is the total on the two dice. Then Y can take values 2, 3, 4, ... 12. Once the dice are rolled the observed value is y.
- Example 2: Hope the Plane Don't Crash Suppose the random variable Y is the number of weeks until the landing gear component is replaced. Then Y can take values 1, 2, 3, 4, ... Once the component is replaced, the number of weeks it lasted is y.
- Probability histograms.
- Relation to density histograms.
- Mean, variance and standard deviation.
- If X=aY+b,
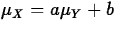
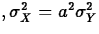 , and
, and 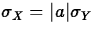 .
. - If
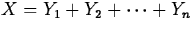 , then
, then
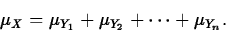
- If Y1 and Y2 are independent random variables for
which variances are defined,
- If Z=Y1+Y2, then
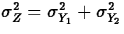 .
. - If W=Y1-Y2, then
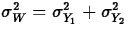 .
.
- If Z=Y1+Y2, then
- If
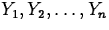 are independent random
variables for which variances are defined, and if
are independent random
variables for which variances are defined, and if
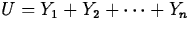 , then
, then
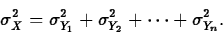
- If
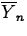 is the sample mean, defined by
is the sample mean, defined by
where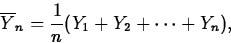
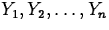 are independent random variables having the
same distribution with mean
are independent random variables having the
same distribution with mean 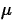 and variance
and variance 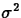 , then
, then
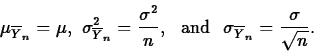
- Binomial trial.
- Binomial random variable.
- Mean, variance and standard deviation.
One stage of a manufacturing process involves a manually-controlled grinding operation. Management suspects that the grinding machine operators tend to grind parts slightly larger rather than slightly smaller than the target diameter, while still staying within specification limits. To verify their suspicions, they sample 150 within-spec parts and find that 93 have diameters above the target diameter. Is this strong evidence in support of their suspicions?
Thus, if there is no tendency to grind to larger or smaller diameters, they would observe as many as 93 of 150 sampled parts having diameters greater than the target in only 21 of 10000 samples.
- Description/use:
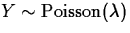 represents the number of occurrences
of some phenomenon in a fixed period of time, area or
space.
represents the number of occurrences
of some phenomenon in a fixed period of time, area or
space. 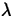 is the mean number of occurrences in that
period of time, area or space. It is used in two settings"
is the mean number of occurrences in that
period of time, area or space. It is used in two settings"
- As an approximation to the b(n,p) model
when n is large and p is small. Take
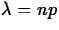 .
. - In its own right following criteria P.1-P.3 on p. 147.
- As an approximation to the b(n,p) model
when n is large and p is small. Take
- Probability mass function:
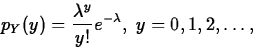
- Mean, variance:
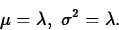
SOLUTION:
The number of transformers that fail within one year is ![]() . Since 250>100, 0.008<0.01 and
. Since 250>100, 0.008<0.01 and ![]() ,we approximate the probability using the Poisson distribution with
,we approximate the probability using the Poisson distribution with
![]() . From Table A.2, p.346, we have
. From Table A.2, p.346, we have ![]() .
.
- Quantifiers of data
- Extend range of conclusions
- Continuous random variable
- Continuous distribution model
- Probability density function
A distribution model for Y, the continuous random variable
describing the lifetime, in hours, of an electronic component,
has a density function pY(y). Since the lifetimes are counted only
for ``burned-in'' components: those that have lasted at least 24
hours, ![]() . It is known that the
probability that the component lasts approximately y1 hours, relative to the
probability that it lasts approximately y2 hours equals (y2/y1)2.
. It is known that the
probability that the component lasts approximately y1 hours, relative to the
probability that it lasts approximately y2 hours equals (y2/y1)2.
- Find pY(y).
- What proportion of all components last between 36 and 48 hours?
- What is the expected value of Y?
- Uniform
- Description/use:
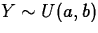 is the value selected ``at random'' from
the interval (a,b).
is the value selected ``at random'' from
the interval (a,b).
- Probability density function:
pY(y) = 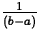 , if a<y<b
, if a<y<b= 0, otherwise. - Mean, variance:
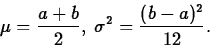
- Description/use:
- Normal
- Description/use:
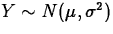 is described by the ``bell curve''.
is described by the ``bell curve''.
- Probability density function:
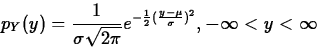
- Mean, variance:
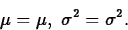
- Description/use:
- Weibull
- Description/use:
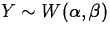 is used as a model of the time to failure of the
first of a number of components.
is used as a model of the time to failure of the
first of a number of components.
- Probability density function:
pY(y) = 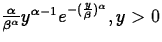 .
.= 0, otherwise. - Mean, variance (when
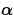 =1):
=1):
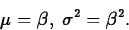
- Description/use:
Assume Y is a continuous random variable with density pY(y).
- Mean
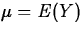 exists if
exists if
In this case,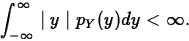
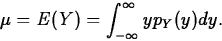
- Variance and standard deviation
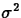 exists if
exists if
In this case,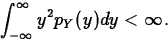
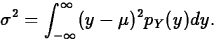
- Probabilities For any set A of real
numbers,
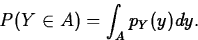
All probabilities from any normal distribution can be reduced to
probabilities from a standard normal (i.e. N(0,1))
distribution. Specifically, if ![]() , then
, then
![]()
![]()
The Central Limit Theorem (CLT) is the most important theorem in statistics. In words, it says:
As long as the population standard deviation is finite, the distribution of the mean (or sum) of independently chosen data from that population gets closer and closer to a normal distribution as the sample size increases.
Suppose that ![]() are independent random variables
having a distribution with mean
are independent random variables
having a distribution with mean ![]() and variance
and variance
![]() . Let
. Let
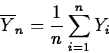
![]()
First note that by multiplying both numerator and denominator by n, we can write
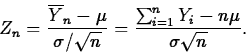
Next, note that if ![]() , we can write
, we can write ![]() ,
where
,
where
![]() are independent Bernoulli(p) random variables.
Since the mean and standard deviation of the Yi are p and
are independent Bernoulli(p) random variables.
Since the mean and standard deviation of the Yi are p and
![]() , respectively, if n is large enough, the CLT says that
, respectively, if n is large enough, the CLT says that
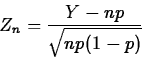
The continuity correction can make the CLT approximation to the binomial more accurate. The continuity correction consists of adding or subtracting 0.5 from the endpoints of the interval:
![]()
![]()
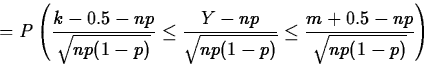
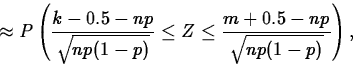
One stage of a manufacturing process involves a manually-controlled grinding operation. Management suspects that the grinding machine operators tend to grind parts slightly larger rather than slightly smaller than the target diameter, while still staying within specification limits. To verify their suspicions, they sample 150 within-spec parts and find that 93 have diameters above the target diameter. Is this strong evidence in support of their suspicions?
And its solution:
Thus, if there is no tendency to grind to larger or smaller diameters, they would observe as many as 93 of 150 sampled parts having diameters greater than the target in only 21 of 10000 samples.
![]()
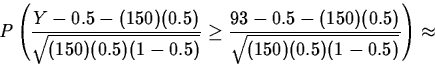
![]()
A quick and simple check: 68-95-99.7 rule.
A Q-Q plot is a plot to decide if it is reasonable to assume a set of data are drawn from a known distribution model (called a candidate distribution model). Suppose Y is a random variable from the candidate distribution model. Then we construct a Q-Q plot as follows:
- 1.
- Order the observations
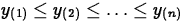 .
.
- 2.
- For each observation compute a
quantile rank with respect to the the candidate distribution
model. For the kth smallest observation, y(k), the quantile
rank is the value q(k) satisfying
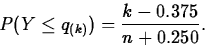
- 3.
- Plot the pairs
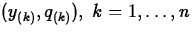 .
.
- If the data are positive and skewed to the right,
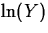 or
or 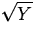 should look more normal.
should look more normal.
- If the data vary by more than 1 or 2 orders of
magnitude, try analyzing
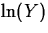 , for positive data, or -1/Y.
, for positive data, or -1/Y.
- If the data consist of counts, try analyzing
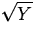 .
. - If the data are proportions and the ratio of the
largest to smallest proportion exceeds 2, try 1the logit
transformation:
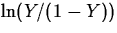 .
.