Recall from chapter 5 that statistical inference is the use of a subset of a population (the sample) to draw conclusions about the entire population. In chapter 5 we studied one kind of inference called estimation. In this chapter, we study a second kind of inference called hypothesis testing.
The validity of inference is related to the way the data are obtained, and to the stationarity of the process producing the data.
- 1.
- The Scientific Hypothesis
- 2.
- The Statistical Model
- 3.
- The Statistical Hypotheses
- 4.
- The Test Statistic
- 5.
- The P-Value
One stage of a manufacturing process involves a manually-controlled
grinding operation. Management suspects that the grinding machine
operators tend to grind parts slightly larger rather than
slightly smaller than the target diameter of 0.75 inches while still
staying within specification limits, which are 0.75 ![]() 0.01 inches.
To verify their suspicions, they sample 150 within-spec parts.
We will use this example to illustrate the components of a statistical
hypothesis testing problem.
0.01 inches.
To verify their suspicions, they sample 150 within-spec parts.
We will use this example to illustrate the components of a statistical
hypothesis testing problem.
- 1.
- The Scientific Hypothesis The scientific
hypothesis is the hypothesized
outcome of the experiment or study. In this example, the
scientific hypothesis is that there is a tendency to grind the
parts larger than the target diameter.
- 2.
- The Statistical Model We will assume these data
were generated by the C+E model:
where the random error,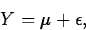
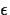 , follows a
, follows a 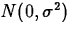 distribution
model.
distribution
model.
- 3.
- The Statistical Hypotheses In terms of the
C+E model, management defined ``a tendency to grind the
parts larger than the target diameter'' to be a statement
about the population mean diameter,
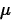 , of the ground parts.
They then defined the statistical hypotheses to be
Notice that Ha states the scientific hypothesis.
, of the ground parts.
They then defined the statistical hypotheses to be
Notice that Ha states the scientific hypothesis.H0: 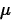
= 0.75 Ha: 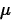
> 0.75 - 4.
- The Test Statistic In all one-parameter hypothesis
test settings
we will consider, the test statistic will be the estimator of
the population parameter about which inference is being made.
As you know from chapter 5, the estimator of
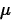 is the sample mean,
is the sample mean,
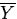 , and this is also the test statistic. The
observed value of
, and this is also the test statistic. The
observed value of 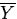 for these data is
for these data is
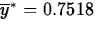 .
. - 5.
- The P-Value Think of this as the plausibility
value. It measures the probability, given that H0 is true,
that a randomly chosen value of the test
statistic will give
as much or more evidence against H0 and in favor of Ha as does
the observed test statistic value.
For the grinding problem, since Ha states that
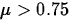 , large values of
, large values of 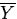 will
provide evidence against H0 and in favor of
Ha. Therefore any value of
will
provide evidence against H0 and in favor of
Ha. Therefore any value of 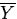 as large or
larger than the observed value
as large or
larger than the observed value 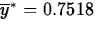 will
provide as much or more evidence against H0 and in favor of
Ha as does the observed test statistic value. Thus,
the p-value is
will
provide as much or more evidence against H0 and in favor of
Ha as does the observed test statistic value. Thus,
the p-value is
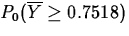 , where P0 is the probability
computed under the assumption that H0 is true: that is,
, where P0 is the probability
computed under the assumption that H0 is true: that is,
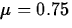 .
.To calculate the p-value, we standardize the test statistic by subtracting its mean (remember we're assuming H0 is true, so we take
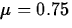 ) and dividing by its
estimated standard error:
) and dividing by its
estimated standard error:
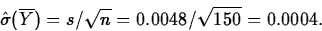
If H0 is true, the result will have a tn-1=t149 distribution.
Putting this all together, the p-value is
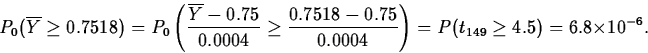
In all examples we'll look at, H0 will be simple (i.e. will state that the parameter has a single value.) as opposed to compound. Alternative hypotheses will be one-sided (that the parameter be larger the null value, or smaller than the null value) or two-sided (that the parameter not equal the null value).
In the grinding example, we had
| H0: | = | 0.75 ( simple) | |
| Ha: | > | 0.75 ( compound, one-sided) |
Suppose in the grinding problem that management wanted to see if the mean diameter was off target. Then appropriate hypotheses would be:
| H0: | = | 0.75 (simple) | |
| Ha: | 0.75 (compound, two-sided) |
In this case, evidence against H0 and in favor of Ha is
provided by both large and small values of ![]() .
.
To compute the p-value of the two-sided test, we first compute the standardized test statistic t, and its observed value, t*:
![]()
Statistical hypothesis testing is modeled on scientific investigation. The two hypotheses represent competing scientific hypotheses.
- The alternative hypothesis is the hypothesis that suggests change, difference or an aspect of a new theory.
- The null hypothesis is the hypothesis that represents the accepted scientific view or that, most often, suggests no difference or effect.
For this reason the null hypothesis is given favored treatment.
- Statistical significance
- Cautions
- o
- Statistical vs. practical significance
- o
- Exploratory vs. confirmatory
- o
- Lotsa tests means false positives
- o
- Data suggesting hypotheses
- o
- Lack of significance
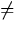 failure
failure
Check out Appendix 6.1, p. 346, with me!
First, check out Appendix 6.1, p. 347, with me!
Example:
Back at the grinding operation, management has decided on another characterization of the scientific hypothesis that ``there is a tendency to grind the parts larger than the target diameter.'' They decide to make inference about p, the population proportion of in-spec parts with diameters larger than the target value. The hypotheses are
| H0: | p | = | 0.5 |
| Ha: | p | > | 0.5 |
The datum is Y, the number of the 150 sampled parts with diameters larger than the target value.
Of the 150 parts, y*=93 (a proportion 0.62) have diameters greater than the target value 0.75.
We will first perform an exact test of these hypotheses. Under H0,
![]() , so the p-value is
, so the p-value is
![]()
Now, for illustration, we will use the large-sample test. This is valid since np0 and n(1-p0) both equal 75>10.
The observed standardized test statistic is
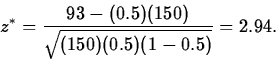
![]()
We assume that there are n1 measurements from population 1 generated by the C+E model
![]()
![]()
We want to compare ![]() and
and ![]() .
.
Sometimes each observation from population 1 is paired with another
observation from population 2. For example, each student may take a pre-
and post-test. In this case n1=n2 and by looking at the pairwise
differences, Di=Y1,i-Y2,i, we transform the two population
problem to a one population problem for C+E model
![]() , where
, where ![]() and
and
![]() . Therefore, an hypothesis test for
the difference
. Therefore, an hypothesis test for
the difference ![]() is obtained by performing a one sample
hypothesis test for
is obtained by performing a one sample
hypothesis test for ![]() based on the differences Di.
based on the differences Di.
The manufacturer of a new warmup bat wants to test its efficacy. To do so, it selects a random sample of 12 baseball players from among a larger number who volunteer to try the bat. For each player, company researchers compute D, the difference between the player's test year average and his previous year's average. Assuming that these differences follow a C+E model, they want to test
| H0: | = | ||
| Ha: | > |
The data (found in SASDATA.BATTING) are:
| PLAYER | AVG92 | AVG93 | DIFFAVG |
| 1 | 0.254 | 0.262 | 0.008 |
| 2 | 0.274 | 0.290 | 0.016 |
| 3 | 0.300 | 0.304 | 0.004 |
| 4 | 0.246 | 0.267 | 0.021 |
| 5 | 0.278 | 0.291 | 0.013 |
| 6 | 0.252 | 0.257 | 0.005 |
| 7 | 0.235 | 0.248 | 0.013 |
| 8 | 0.313 | 0.324 | 0.021 |
| 9 | 0.305 | 0.317 | 0.012 |
| 10 | 0.255 | 0.252 | -0.003 |
| 11 | 0.244 | 0.276 | 0.032 |
| 12 | 0.322 | 0.332 | 0.010 |
An inspection of the differences shows no evidence of nonnormality or
outliers, so we proceed with the test. For these data,
![]() , and sd=0.0092.
Then
, and sd=0.0092.
Then ![]() , so the
observed value of the standardized test statistic is
, so the
observed value of the standardized test statistic is
![]()
![]()
Let ![]() and
and ![]() denote the sample
means from populations 1 and 2,
S12 and S22 the
sample variances.
The point estimator of
denote the sample
means from populations 1 and 2,
S12 and S22 the
sample variances.
The point estimator of ![]() , is
, is
![]() . We will test
. We will test
| H0: | = | ||
| Versus one of | |||
| Ha-: | < | ||
| Ha+: | < | ||
If the population variances are equal
(![]() ), then
we estimate
), then
we estimate ![]() by the pooled variance estimator
by the pooled variance estimator
![]()
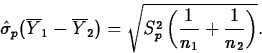
Then, if H0 is true,
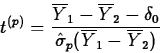
Suppose t(p)* is the observed value of t(p). Then the p-value of the test of H0 versus Ha- is
![]()
![]()
![]()
If ![]() , then the standardized test statistic
, then the standardized test statistic
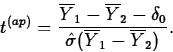
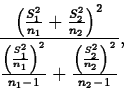
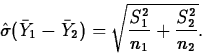
If t(ap)* denotes the observed value of t(ap), the
p-values for H0 versus Ha-, Ha+ and ![]() ,
respectively, are
,
respectively, are ![]() ,
,
![]() and
and ![]() .
.
Example:
A company buys cutting blades used in its manufacturing process from two suppliers. In order to decide if there is a difference in blade life, the lifetimes of 10 blades from manufacturer 1 and 13 blades from manufacturer 2 used in the same application are compared. A summary of the data shows the following (units are hours): (The data are in SASDATA.BLADE2)
| Manufacturer | n | s | |
| 1 | 10 | 118.4 | 26.9 |
| 2 | 13 | 134.9 | 18.4 |
The experimenters want to test
| H0: | = | ||
| Ha: |
The experimenters generated histograms and normal quantile plots of
the two data sets and found no evidence of nonnormality or outliers.
The estimate of ![]() is
is ![]() .
.
- Pooled variance test
The pooled variance estimate is
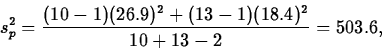
So the standard error estimate of
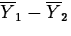 is
is
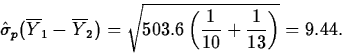
Therefore, t(p)*=-16.52/9.44=-1.75, with 21 degrees of freedom. So
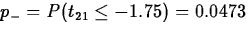 ,
, 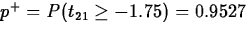 ,
and the p-value for this problem is
,
and the p-value for this problem is 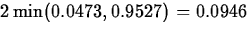 .
. - Separate variance test
The standard error estimate of
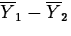 is
is
The observed value of the standardized test statistic is t(ap)*=-16.52/9.92=-1.67. The degrees of freedom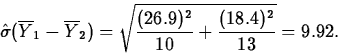
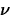 is computed as the greatest integer less than
or equal to
is computed as the greatest integer less than
or equal to
so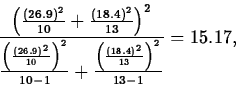
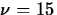 .
.Therefore,
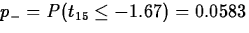 ,
, 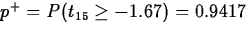 ,
and the p-value for this problem is
,
and the p-value for this problem is
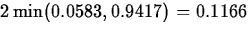 .
.The results for the two t-tests are not much different.
![]() and
and ![]() are observations from
two independent populations. The estimator of p1-p2 is
are observations from
two independent populations. The estimator of p1-p2 is
![]()
We wish to test a null hypothesis that the two population proportions
differ by a known amount ![]() ,
,
| H0: | p1-p2 | = |
| Ha+: | p1-p2 | > | |
| Ha-: | p1-p2 | < | |
| p1-p2 |
Case 1: 0
Suppose H0 is p1-p2=0. Then, let p=p1=p2 denote the common
value of the two population proportions. If H0 is true, the
variance of ![]() equals p(1-p)/n1 and that of
equals p(1-p)/n1 and that of
![]() equals p(1-p)/n2. This implies the standard error of
equals p(1-p)/n2. This implies the standard error of
![]() equals
equals
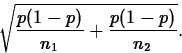
Since we don't know p, we estimate it using the data from both populations:
![]()
The estimated standard error of ![]() is then
is then
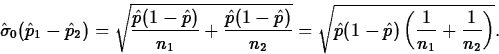
The standardized test statistic is then
![]()
Case 2: 0
If ![]() ,
the (by now) standard reasoning gives the standardized test statistic
,
the (by now) standard reasoning gives the standardized test statistic
![]()
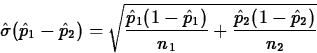
In a recent survey on academic dishonesty 24 of the 200 female college students surveyed and 26 of the 100 male college students surveyed agreed or strongly agreed with the statement ``Under some circumstances academic dishonesty is justified.'' Suppose pf denotes the proportion of all female and pm the proportion of all male college students who agree or strongly agree with this statement.
- If we want to Test
H0: pf-pm = Ha: pf-pm 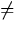
Since Yf=24, 200-Yf=176, Ym=26, and 100-Ym=74 all exceed 10, we may use the normal approximation.
The point estimate of pf-pm is
and the estimate of the common value of pf and pm under H0 is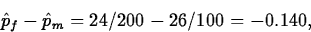
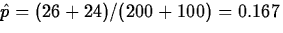 .
.Thus,
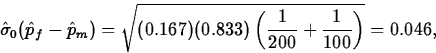
and
From this, we obtain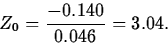
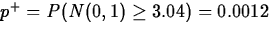 ,
,
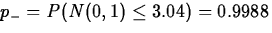 , and
, and
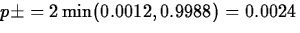 , this last being the p-value we want.
, this last being the p-value we want.
- If we want to test
H0: pf-pm = -0.10 Ha: pf-pm < -0.10 The estimated standard error of pf-pm is
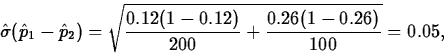
which gives
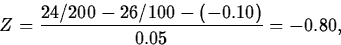
and a p-value of
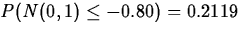 .
.
Steps, illustrated using grinding example:
- 1.
- Specify hypotheses to be tested.
(i.e.
H0: 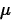
= 0.75 Ha: 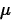
> 0.75 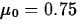 )
)
- 2.
- Set the significance level . Usual choices
are 0.01 or 0.05. We'll choose the latter.
- 3.
- Specify the (standardized) test statistic and it's
distribution under H0. For simplicity, assume we know
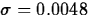 . Then the standardized test statistic is
. Then the standardized test statistic is
and under H0 it has a N(0,1) distribution.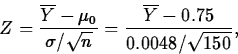
- 4.
- Find the critical region of the test. The
critical region of the test is the set of values of the (standardized)
test statistic for which H0 will be rejected in favor of
Ha. Here, Ha tells us that the critical region has the form
meaning H0 will be rejected if and only if the observed value of Z is greater than or equal to 1.645.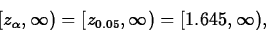
- 5.
- Perform the test. The observed value of Z is
which falls in the critical region, so H0 is rejected in favor of Ha.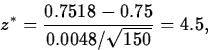
In the grinding example, the power is
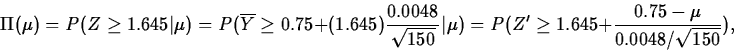
where ![]() .
.