• Bivariate Data: Graphical Display

  The scatterplot is the basic tool for graphically displaying bivariate quantitative data.

  Example:

  Some investors think that the performance of the stock market in January is a good predictor of its performance for the entire year. To see if this is true, consider the following data on Standard & Poor's 500 stock index (found in SASDATA.SANDP).

  Percent Percent

  January 12 Month

  Year Gain Gain

  1985 7.4 26.3

  1986 0.2 14.6

  1987 13.2 2.0

  1988 4.0 12.4

  1989 7.1 27.3

  1990 -6.9 -6.6

  1991 4.2 26.3

  1992 -2.0 4.5

  1993 0.7 7.1

  1994 3.3 -1.5

  Figure 1 shows a scatterplot of the percent gain in the S&P index over the year (vertical axis) versus the percent gain in January (horizontal axis). Each point is labelled with its corresponding year.
  

   

  Figure:

  
  
  
• How to analyze a scatterplot

  The scatterplot of the S&P data can illustrate the general analysis of scatterplots. You should look for:

  • Association. This is a pattern in the scatterplot.
  • Type of Association. If there is association, is it:

    o

    Linear.

    o

    Nonlinear.

  • Direction of Association.

  For the S&P data, there is association. This shows up as a general positive relation (Larger % gain in January is generally associated with larger % yearly gain.) It is hard to tell if the association is linear, since the spread of the data is increasing with larger January % gain. This is due primarily to the 1987 datum in the lower right corner of plot, and to some extent the 1994 datum. Eliminate those two points, and the association is strong linear and positive, as Figure 2 shows.
  

   

  Figure:

  
  
  

  There is some justification for considering the 1987 datum atypical. That was the year of the October stock market crash. The 1994 datum is a mystery to me.

• Data Smoothers

  Data smoothers can help identify and simplify patterns in large sets of bivariate data. You have already met one data smoother: the moving average.

  Another is the median trace.

• Correlation

  Pearson Correlation

  Suppose n measurements, $(X_i,\; Y_i), \; i=1, \ldots ,n$ are taken on the variables X and Y. Then the Pearson correlation between X and Y computed from these data is

  $$r=\frac{1}{n-1} \sum_{i=1}^{n}X_{i}^{\prime} Y_{i}^{\prime},$$

  where

  $$X_{i}^{\prime}=\frac{X_i-\overline{X}}{S_X} \mbox{ and } Y_{i}^{\prime}=\frac{Y_i-\overline{Y}}{S_Y}$$

  are the standardized data.
• Good Things to Know About Pearson Correlation
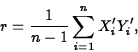
  • Pearson correlation is always between -1 and 1. Values near 1 signify strong positive linear association. Values near -1 signify strong negative linear association. Values near 0 signify weak linear association.
  • Correlation between X and Y is the same as the correlation between Y and X.
  • Correlation can never by itself adequately summarize a set of bivariate data. Only when used in conjunction with 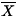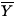$\overline{X}$, $\overline{Y}$, S_X, and S_Y and a scatterplot can an adequate summary be obtained.
  • The meaningfulness of a correlation can only be judged with respect to the sample size.
• A Confidence Interval for the Population Correlation, $\rho$

  If n is the sample size,

  $$t=(r-\rho) \sqrt{\frac{n-2}{(1-r^2)(1-\rho^2)}}$$

  has approximately a t_n-2 distribution. We can use this fact to obtain a confidence interval for $\rho$.

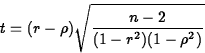
  Example:

  Back to the S&P data, the SAS macro CORR gives a 95% confidence interval for $\rho$ as
  (-0.2775,  0.8345). As this interval contains 0, it indicates no significant linear association between JANGAIN and YEARGAIN.

  If we remove the 1987 and 1994 data, a different story emerges. Then the Pearson correlation is r=0.9360, and a 95% confidence interval for $\rho$ is (0.6780, 0.9880). Since this interval consists entirely of positive numbers, we conclude that $\rho$ is positive and we estimate its value to be between 0.6780 and 0.9880.

  QUESTION: What is $\rho$? Does this make sense?

• Simple Linear Regression

  The SLR model attempts to quantify the relationship between a single predictor variable Z and a response variable Y. This reasonably flexible yet simple model has the form

  $$Y=\beta_0+\beta_1X(Z)+\epsilon,$$

  where $\epsilon$ is a random error term, and X(Z) is a function of Z, such as Z, Z², or $\ln(Z)$.

  By looking at different functions X, we are not confined to linear relationships, but can also model nonlinear ones. The function X is called the regressor. Often, we omit specifying the dependence of the regressor X on the predictor Z, and just write the model as

  $$Y=\beta_0+\beta_1X+\epsilon.$$

  We want to fit the model to a set of data $(X_i,Y_i), \; i=1, \ldots, n$. As with the C+E model, two options are least absolute errors, which finds values b₀ and b₁ to minimize

  $$\mbox{SAE}(b_{0},b_{1})=\sum_{i=1}^{n} \mid Y_{i}-(b_0+b_1X_{i}) \mid,$$

  or least squares, which finds values b₀ and b₁ to minimize

  $$\mbox{SSE}(b_{0},b_{1})=\sum_{i=1}^{n}(Y_{i}-(b_0+b_1X_{i}))^{2}.$$

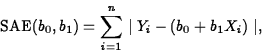
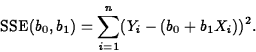
  We'll concentrate on least squares. Using calculus, we find the least squares estimators of $\beta_0$ and $\beta_1$ to be

  $$\hat{\beta}_1=\frac{\sum_{i=1}^n (X_i-\overline{X})(Y_i-\overline{Y})}{\sum_{i=1}^n (X_i-\overline{X})^2}.$$

  and

  $$\hat{\beta}_0=\overline{Y}-\hat{\beta}_1\overline{X}.$$

• Example: For the S&P data, we would like to fit a model that can predict YEARGAIN (the response) as a function of JANGAIN (the predictor). Since a scatterplot reveals no obvious nonlinearity, we will take the regressor to equal the predictor.

  The relevant SAS/INSIGHT output for the regression of YEARGAIN on JANGAIN is shown in Figure 3.

  
  

   

  Figure:

  
  
  And the relevant SAS/INSIGHT output for the regression of YEARGAIN on JANGAIN, with the years 1987 and 1994 removed, is shown in Figure 4.

  
  

   

  Figure:

  
  
  
• Residuals, Predicted and Fitted Values
  • The predicted value of Y at X is

    $$\hat{Y}=\hat{\beta}_0+\hat{\beta}_1 X.$$

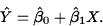
  • For X=X_i, one of the values in the data set, the predicted value is called a fitted value and is written

    $$\hat{Y}_i=\hat{\beta}_0+\hat{\beta}_1 X_i.$$

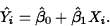
  • The residuals, 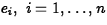$e_i,~ i=1, \ldots, n$ are the differences between the observed and fitted values for each data value:

    $$e_i=Y_i-\hat{Y}_i=Y_i-(\hat{\beta}_0+\hat{\beta}_1 X_i).$$

• Tools to Assess the Quality of the Fit
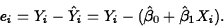
  • Residuals. Residuals should exhibit no patterns when plotted versus the X_i, 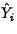$\hat{Y}_i$ or other variables, such as time order. Studentized residuals should be plotted on a normal quantile plot.
  • Coefficient of Determination. The coefficient of determination, r², is a measure of (take your pick):

    o

    How much of the variation in the response is ``explained'' by the predictor.

    o

    How much of the variation in the response is reduced by knowing the predictor.

  The notation r² comes from the fact that the coefficient of determination is the square of the Pearson correlation. Check out the quality of the two fits for the S&P data:
• Model Interpretation
  • The Fitted Slope. The fitted slope may be interpreted in a couple of ways:

    o

    As the estimated change in the mean response per unit increase in the regressor. This is another way of saying it is the derivative of the fitted response with respect to the regressor:

    $$\frac{d\hat{Y}}{dx}=\frac{d}{dx}(\hat{\beta}_0+\hat{\beta}_1x)= \hat{\beta}_1.$$

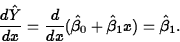
    o

    In terms of the estimated change in the mean response per unit increase in the predictor. In this formulation, if the regressor X, is a differentiable function of the predictor, Z,

    $$\frac{d\hat{Y}}{dz}=\frac{d}{dz}(\hat{\beta}_0+\hat{\beta}_1X)= \hat{\beta}_1\frac{dX}{dz},$$

    so

    $$\hat{\beta}_1=\frac{d\hat{Y}}{dz}\left/\frac{dX}{dz}\right.$$

  • The Fitted Intercept. The fitted intercept is the estimate of the response when the regressor equals 0, provided this makes sense.
  • The Mean Square Error. The mean square error or MSE, is an estimator of the variance of the error terms $\epsilon$,in the simple linear regression model. Its formula is

    $$\mbox{MSE}=\frac{1}{n-2}\sum_{i=1}^ne_i^2.$$

    It measures the ``average squared prediction error'' when using the regression.

• Example: Consider the S&P data with the 1987 and 1994 observations omitted. The fitted model is

  $$\widehat{YEARGAIN}=9.6462+2.3626 JANGAIN.$$

  • The Fitted Slope. The fitted slope, 2.3626 is interpreted as the estimated change in YEARGAIN per unit increase in JANGAIN.
  • The Fitted Intercept. The fitted intercept, 9.6462, is the estimated YEARGAIN if JANGAIN equals 0.
  • The Mean Square Error. The MSE, 21.59, estimates the variance of the random errors.

• Classical Inference for the SLR Model

  Estimation of Slope and Intercept

  Level L confidence intervals for $\beta_0$ and $\beta_1$ are

  $$(\hat{\beta}_0-\hat{\sigma}(\hat{\beta}_0)t_{n-2,\frac{1+L}{... ...hat{\beta}_0+\hat{\sigma}(\hat{\beta}_0)t_{n-2,\frac{1+L}{2}}),$$

  and

  $$(\hat{\beta}_1-\hat{\sigma}(\hat{\beta}_1)t_{n-2,\frac{1+L}{... ...hat{\beta}_1+\hat{\sigma}(\hat{\beta}_1)t_{n-2,\frac{1+L}{2}}),$$

  respectively, where

  $$\hat{\sigma}(\hat{\beta}_0)=\sqrt{\mbox{MSE} \left/ \left[\f... ...rline{X}^2}{\sum_{i=1}^n(X_i-\overline{X})^2}\right]\right .} ,$$

  and

  $$\hat{\sigma}(\hat{\beta}_1)=\sqrt{\mbox{MSE} \left/\sum_{i=1}^n(X_i-\overline{X})^2\right .}$$

• Example: For the reduced S&P data (i.e. with 1987 and 1994 removed) the SAS/INSIGHT output shows the estimated intercept is $\hat{\beta}_0=9.65$ with $\hat{\sigma}(\hat{\beta}_0)=1.77$. Since t_6,0.975=2.45, a 95% confidence interval for $\beta_0$ is

  $$9.65\pm (1.77)(2.45)=(5.31,13.98).$$

  A similar computation with $\hat{\beta}_1=2.36$ and $\hat{\sigma}(\hat{\beta}_1)=0.36$, gives a 95% confidence interval for $\beta_1$ as

  $$2.36\pm (0.36)(2.45)=(1.47,3.25).$$

  NOTE: Whether the interval for $\beta_1$ contains 0 is of particular interest. If it does, it means that we cannot statistically distinguish $\beta_1$ from 0. This means we have to consider plausible the model for which $\beta_1=0$:

  $$Y=\beta_0+\epsilon$$

  This model, which is just the C+E model, implies that there is no association between Y and X.
• Estimation of The Mean Response

  The mean response at X=x₀ is

  $$\mu_0=\beta_0+\beta_1 x_0.$$

  The point estimator of $\mu_0$ is

  $$\hat{Y}_0=\hat{\beta}_0+\hat{\beta}_1 x_0.$$

  A level L confidence interval for $\mu_0$ is

  $$(\hat{Y}_0-\hat{\sigma}(\hat{Y}_0)t_{n-2,\frac{1+L}{2}} ,\hat{Y}_0+\hat{\sigma}(\hat{Y}_0) t_{n-2,\frac{1+L}{2}}),$$

  where

  $$\hat{\sigma}(\hat{Y}_0)=\sqrt{\mbox{MSE}\left[\frac{1}{n}+\frac{(x_0-\overline{X})^2}{\sum(X_i-\overline{X})^2}\right]}.$$

• Prediction of a Future Observation

  A level L prediction interval for a future observation at X=x₀ is

  $$(\hat{Y}_{new}-\hat{\sigma}(Y_{new}-\hat{Y}_{new})t_{n-2,\frac{1+L}{2}},$$

  $$\hat{Y}_{new}+ \hat{\sigma}(Y_{new}-\hat{Y}_{new})t_{n-2,\frac{1+L}{2}})),$$

  where

  $$\hat{Y}_{new}=\hat{\beta}_0+\hat{\beta}_1 x_0,$$

  and

  $$\hat{\sigma}(Y_{new}-\hat{Y}_{new})=\sqrt{\mbox{MSE}\left[1+... ...+\frac{(x_0-\overline{X})^2}{\sum(X_i-\overline{X})^2}\right]}.$$

  The macro REGPRED will compute confidence intervals for a mean response and prediction intervals for future observations for each data value and for other user-chosen X values.

• Example:

  The SAS macro REGPRED was run on the reduced S&P data, and estimation of the mean response and prediction of a new observation at the value JANGAIN=5 were requested. Both $\hat{Y}_0$ and $\hat{Y}_{new}$equal 9.65+(2.36)(5)=21.46. The macro computes a 95% confidence interval for the mean response at JANGAIN=5 as (16.56,26.36), and a 95% prediction interval for a new observation at JANGAIN=5 as (9.08,33.84).

• The Relation Between Correlation and Regression

  If the standardized responses and regressors are

  $$Y'_i=\frac{Y_i-\overline{Y}}{S_Y},$$

  and

  $$X'_i=\frac{X_i-\overline{X}}{S_X},$$

  Then the regression equation fitted by least squares can be written as

  $$\hat{Y'}=r \cdot X',$$

  Where X' is any value of a regressor variable standardized as described above.

  The Regression Effect refers to the phenomenon of the standardized predicted value being closer to 0 than the standardized regressor. Equivalently, the unstandardized predicted value is fewer Y standard deviations from the response mean than the regressor value is in X standard deviations from the regressor mean.

  For the S&P data r=0.4295, so for a January gain $X^\prime$standard deviations (S_X) from $\overline{X}$, the regression equation estimates a gain for the year of

  $$\hat{Y'}=0.4295 \cdot X'$$

  standard deviations (S_Y) from $\overline{Y}$.

  With 1987 and 1994 removed, the estimate is

  $$\hat{Y'}=0.9360 \cdot X',$$

  which reflects the stronger relation.
• The Relationship Between Two Categorical Variables

  Analysis of categorical data is based on counts, proportions or percentages of data that fall into the various categories defined by the variables.

  Some tools used to analyze bivariate categorical data are:

  • Mosaic Plots.
  • Two-Way Tables.
• Example:
  

  A survey on academic dishonesty was conducted among WPI students in 1993 and again in 1996. One question asked students to respond to the statement ``Under some circumstances academic dishonesty is justified.'' Possible responses were ``Strongly agree'', ``Agree'', ``Disagree'' and ``Strongly disagree''. The 1993 results are shown in the following 2x2 table and in the mosaic plots in Figure 5 and 6:

   

  Row Pct. Strongly

  Col Pct. Agree Disagree Disagree Total

  Male 31 71 30 132

  17.32 39.66 16.76 73.74

  23.48 53.79 22.73

  65.96 79.78 69.77 Gender

  Female 16 18 13 47

  8.94 10.06 7.26 26.26

  34.04 38.30 27.66

  34.04 20.22 30.23

  Total 47 89 43 179

  26.26 49.72 24.02 100.00

  
  

   

  Figure:

  

  
  
  

   

  Figure:

  

  
  

  Inference for Categorical Data with Two Categories Methods for comparing two proportions can be used (estimation from chapter 5 and hypothesis tests from chapter 6).

  Inference for Categorical Data with More Than Two Categories: One-Way Tables

  Suppose the categorical variable has c categories, and that the population proportion in category i is p_i. To test

   

  $$p_i^{(0)},~ i=1,2, \ldots, c$$ H₀: p_i =

  $$\neq p_i^{(0)} \mbox{ for at least one } i$$ H_a: p_i

  for pre-specified values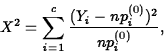 $p_i^{(0)}, i=1,2, \ldots, c,$ use the Pearson $\mbox{{\boldmath${\chi}$}}$² statistic

  $$X^2 = \displaystyle \sum_{i=1}^c \frac{(Y_i-np_i^{(0)})^2}{np_i^{(0)}},$$

  where Y_i is the observed frequency in category i, and n is the total number of observations.

  Note that for each category the Pearson statistic computes (observed-expected)²/expected and sums over all categories.

  Under H₀, $X^2\sim \chi^2_{c-1}$. Therefore, if x^2* is the observed value of X², the p-value of the test is $P(\chi^2_{c-1}\geq x^{2*})$.

  Example:
  Historically, the distribution of weights of ``5 pound'' dumbbells produced by one manufacturer have been normal with mean 5.01 and standard deviation 0.15 pound. It can be easily shown that 20% of the area under a normal curve lies within $\pm 0.25$ standard deviations of the mean, 20% lies between 0.25 and 0.84 standard deviations of the mean, 20% lies between -0.84 and -0.25 standard deviations of the mean, 20% lies beyond 0.84 standard deviations above the mean, and another 20% lies beyond 0.84 standard deviations below the mean.

  This means that the boundaries that break the N(5.01,0.15²) density into five subregions, each with area 0.2, are 4.884, 4.9725, 5.0475 and 5.136.

  A sample of 100 dumbbells from a new production lot shows that 25 lie below 4.884, 23 between 4.884 and 4.9725, 21 between 4.9725 and 5.0475, 18 between 5.0475 and 13 above 5.136. Is this good evidence that the new production lot does not follow the historical weight distribution?

  Solution:
  We will perform a $\chi^2$ test. Let p_i be the proportion of dumbbells in the production lot with weights in subinterval i, where subinterval 1 is $(-\infty,4.884]$, subinterval 2 is (4.884,4.9725], and so on. If the production lot follows the historical weight distribution, all p_i equal 0.2. This gives our hypotheses:

  $$0.2,~ i=1,2, \ldots, 5$$ H₀: p_i =

  $$\neq$$ H_a: p_i 0.2,

  for at least one $i,\; i=1,2,\ldots, 5$.

  Since np⁽⁰⁾_i=20 for each i, the test statistic is

  $$x^{2*} = \frac{(25-20)^2}{20} + \ldots + \frac{(13-20)^2}{20}=4.4$$

  The p-value is $P(\chi^2_4\geq 4.4)=0.3546$, so we cannot reject H₀.

  Inference for Categorical Data with More Than Two Categories: Two-Way Tables Suppose a population is partitioned into rc categories, determined by r levels of variable 1 and c levels of variable 2. The population proportion for level i of variable 1 and level j of variable 2 is p_ij. These can be displayed in the following $r\times c$ table:

  Column Marginals

  row 1 2 ... c

  $$p_{1\cdot}$$ 1 p₁₁ p₁₂ ... p_1c

  $$p_{2\cdot}$$ 2 p₂₁ p₂₂ ... p_2c

  . . . . .

  . . . . .

  . . . . .

  $$p_{r\cdot}$$ r p_r1 p_r2 ... p_rc

  $$p_{\cdot 1} p_{\cdot 2} p_{\cdot c}$$ Marginals ... 1

  We want to test

  H₀: row and column variables are independent

  H_a: row and column variables are not independent.

  To do so, we select a random sample of size n from the population. Suppose the table of observed frequencies is

  Column Totals

  row 1 2 ... c

  $$Y_{1\cdot}$$ 1 Y₁₁ Y₁₂ ... Y_1c

  $$Y_{2\cdot}$$ 2 Y₂₁ Y₂₂ ... Y_2c

  . . . . .

  . . . . .

  . . . . .

  $$Y_{r\cdot}$$ r Y_r1 Y_r2 ... Y_rc

  $$Y_{\cdot 1} Y_{\cdot 2} Y_{\cdot c}$$ Totals ... n

  Under H₀ the expected cell frequencies are given by

  $$\mbox{expected value} = \frac{ \mbox{row total} \times \mbox{column total} }{\mbox{sample size}}.$$

  To measure the deviations of the observed frequencies from the expected frequencies under the assumption of independence, we construct the Pearson $\chi^2$ statistic

  $$X^2 = \displaystyle \sum_{i=1}^r \sum_{j=1}^{c} \frac{(Y_{i... ...dot}\hat{p}_{\cdot j})^2}{n\hat{p}_{i\cdot}\hat{p}_{\cdot j}},$$

  where $\hat{p}_{i\cdot}=Y_{i\cdot}/n$ and $\hat{p}_{\cdot j}=Y_{\cdot j}/n$.

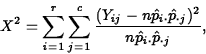
  Note that for the test to be valid, we require that $np_{i\cdot}p_{\cdot j}\geq 5$.

  Example: A polling firm surveyed 269 American adults concerning how leisure time is spent in the home. One question asked them to select which of five leisure activities they were most likely to partake in on a weeknight. The results are broken down by age group in the following table, in which the cell entries are frequency, expected frequency under the hypothesis of independence of age and activity, and Pearson residual.

  	Activity
  Age	Watch		Listen	Listen	Play Computer	Totals
  Group	TV	Read	to Radio	to Stereo	Game	Totals
  18-25	21	3	9	10	19	62
  	(19.13)	(9.22)	(11.52)	(11.75)	(10.37)
  	(+0.43)	(-2.05)	(-0.74)	(-0.51)	(+2.68)
  26-35	17	5	6	8	13	49
  	(15.12)	(7.29)	(9.11)	(9.29)	(8.20)
  	(0.48)	(-0.85)	(-1.03)	(-0.42)	(1.68)
  36-50	14	8	8	12	9	51
  	(15.74)	(7.58)	(9.48)	(9.67)	(8.53)
  	(-0.44)	(0.15)	(-0.48)	(0.75)	(0.16)
  51-65	18	10	11	10	3	52
  	(16.04)	(7.73)	(9.67)	(9.86)	(8.70)
  	(0.49)	(0.82)	(0.43)	(0.04)	(-1.93)
  Over 65	13	14	16	11	1	55
  	(16.97)	(8.18)	(10.22)	(10.43)	(9.20)
  	(-0.96)	(2.04)	(1.81)	(0.18)	(-2.70)
  Totals	83	40	50	51	45	269

  As an example of the computation of table entries, consider the entries in the (1,2) cell (age: 18-25, activity: Read), in which the observed frequency is 3. The marginal number in the 18-25 bracket is 62, while the marginal number in the Read bracket is 40, so $\hat{p}_{1\cdot}=62/269$, while $\hat{p}_{\cdot 2}=40/269$, so the expected number in the (1,2) cell is 269(62/269)(40/269)=9.22. The Pearson residual is $(3-9.22)/\sqrt(9.22)=-2.05$. The value of the chi-square statistic is 38.91, which is computed as the sum of the squares of the Pearson residuals. Comparing this with the chi-square distribution with 16 degrees of freedom, we get a p-value of 0.0011.

  Association is NOT Cause and Effect

  Two variables may be associated due to a number of reasons, such as:

  1.

  X could cause Y.

  2.

  Y could cause X.

  3.

  X and Y could cause each other.

  4.

  X and Y could be caused by a third (lurking) variable Z.

  5.

  X and Y could be related by chance.

  6.

  Bad (or good) luck.

  The Issue of Stationarity

  • When assessing the stationarity of a process in terms of bivariate measurements X and Y, always consider the evolution of the relationship between X and Y, as well as the individual distribution of the X and Y values, over time or order.
  • Suppose we have a model relating a measurement from a process to time or order. If, as more data are taken the pattern relating the measurement to time or order remains the same, we say that the process is stationary relative to the model.

About this document ...

This document was generated using the LaTeX2HTML translator Version 97.1 (release) (July 13th, 1997)

Copyright © 1993, 1994, 1995, 1996, 1997, Nikos Drakos, Computer Based Learning Unit, University of Leeds.

The command line arguments were:
latex2html -split 0 lect7.

The translation was initiated by Joseph D Petruccelli on 11/4/1999