![]()
![]()
![]()
![]()
We will write these models generically as
![]()
The surface defined by the deterministic part of the multiple linear regression model,
![]()
![]()
![]()
When considered a function of the regressors, the response surface is defined by the functional relationship
![]()
![]()
If it is possible for
the Xi to simultaneously take the value 0, then ![]() is the
value of the response surface when all Xi equal 0. Otherwise,
is the
value of the response surface when all Xi equal 0. Otherwise,
![]() has no separate interpretation of its own.
has no separate interpretation of its own.
As a function of the predictors, the response surface is defined by the functional relationship
![]()
![]()
![]()
![]()
![]()
- o
- Additive Model: For the
model
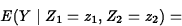
the change in expected response per unit change in zi is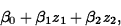
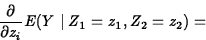
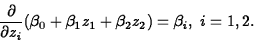
- o
- Full Quadratic Model: For the full
quadratic model
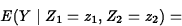
the change in expected response per unit change in z1 is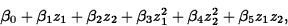
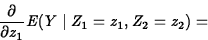
and the change in expected response per unit change in z2 is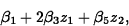
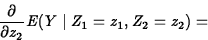
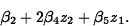
The modeling process involves the following steps:
- 1.
- Model Specification
- 2.
- Model Fitting
- 3.
- Model Assessment
- 4.
- Model Validation
Multivariable visualization begins with a number of standard statistical tools, such as histograms, to look at each variable individually, or scatterplots, to look at pairs of variables. But the true power of multivariable visualization can be found only in a set of sophisticated statistical tools which make use of multiple dynamically-linked displays (You won't find these in Microsoft Excel!) Two such tools are
- Scatterplot Arrays
- Rotating 3-D Plots
- 1.
-
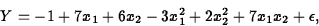
- 2.
-
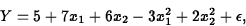
- 3.
-
- 4.
-
Now use the rotating 3-D plot to view the data. Does this change your guesses?
As we did for SLR model, we use least squares to fit the MLR
model. This means finding estmators of the model parameters
![]() and
and ![]() . The LSEs of the
. The LSEs of the
![]() s are those values, of
s are those values, of ![]() , denoted
, denoted
![]() ,
which minimize
,
which minimize
![]()
![\begin{displaymath}
\sum_{i=1}^n[Y_i-(b_0+b_1 X_{i1}+b_2 X_{i2}+\cdots +b_q X_{iq})]^2.\end{displaymath}](img41.gif)
![]()
![]()
Example:
Let's see what happens when we fit identify and fit a model to data in sasdata.cars93a.
![\begin{figure}
\centerline{\includegraphics*[height=5in,width=5in]{lect8o1.eps}}
\end{figure}](img44.gif)
Residuals and studentized residuals are the primary tools to analyze model fit. We look for outliers and other deviations from model assumptions.
Example:
Let's look at the residuals from the fit to the data in sasdata.cars93a.
![\begin{figure}
\centerline{\includegraphics*[height=5in,width=5in]{lect8o2.eps}}
\end{figure}](img45.gif)
![\begin{figure}
\centerline{\includegraphics*[height=5in,width=5in]{lect8o3.eps}}
\end{figure}](img46.gif)
The fitted model is
![]()
![]()
![]()
If we feel that this model fits the data well, then for purposes of interpretation, we regard the fitted model as the actual response surface, and we interpret it exactly as we would interpret the response surface.
Example:
Let's interpret the fitted model for the fit to the data in sasdata.cars93a.
Two ways of building models:
- Empirical modeling
- Theoretical modeling
- Residual analysis
- Principle of parsimony (simplicity of description)
- Coefficient of multiple determination, and its adjusted cousin.
Example:
Let's fit a second model to the data in sasdata.cars93a, and compare its fit to the first model we considered.
![\begin{figure}
\centerline{\includegraphics*[height=5in,width=5in]{lect8o6.eps}}
\end{figure}](img50.gif)
![\begin{figure}
\centerline{\includegraphics*[height=5in,width=5in]{lect8o7.eps}}
\end{figure}](img51.gif)
![\begin{figure}
\centerline{\includegraphics*[height=5in,width=5in]{lect8o8.eps}}
\end{figure}](img52.gif)
Idea:
- Total variation in the response (about its mean) is
measured by
This is the variation or uncertainty of prediciton if no predictor variables are used.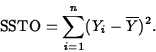
- SSTO can be broken down into two pieces: SSR, the regression sum of squares, and SSE, the error sum of squares, so that SSTO=SSR+SSE.
-
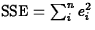 is the total sum of the squared
residuals. It measures the variation of the response unaccounted for
by
the fitted model or, equivalently, the uncertainty of predicting the response using
the
fitted model.
is the total sum of the squared
residuals. It measures the variation of the response unaccounted for
by
the fitted model or, equivalently, the uncertainty of predicting the response using
the
fitted model.
-
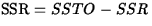 is the variability explained by
the
fitted model or, equivalently, the reduction in uncertainty of prediction due to
using
the fitted model.
is the variability explained by
the
fitted model or, equivalently, the reduction in uncertainty of prediction due to
using
the fitted model.
The degrees of freedom for a SS is the number of independent pieces of data making up the SS. For SSTO, SSE and SSR the degrees of freedom are n-1, n-q-1 and q. These add just as the SSs do. A SS divided by its degrees of freedom is called a Mean Square.
This is a table which summarizes the SSs, degrees of freedom and mean squares.
Example:
Here's the ANOVA table for the original fit to the sasdata.cars93a data.
![\begin{figure}
\centerline{\includegraphics*[height=5in,width=5in]{lect8o1.eps}}
\end{figure}](img44.gif)
- The Hypotheses:
H0: 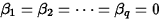
Ha: Not H0 - The Test Statistic: F=MSR/MSE
- The P-Value: P(Fq,n-q-1>F*), where Fq,n-q-1 is a random variable from an Fq,n-q-1 distribution and F* is the observed value of the test statistic.
- The Hypotheses:
H0: 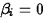
Ha: 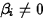
- The Test Statistic:
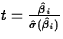
- The P-Value: P(|tn-q-1|>|t*|), where tn-q-1 is a random variable from a tn-q-1 distribution and t* is the observed value of the test statistic.
Example:
Here are the tests for the original fit to the sasdata.cars93a data.
![\begin{figure}
\centerline{\includegraphics*[height=5in,width=5in]{lect8o1.eps}}
\end{figure}](img44.gif)
- Confidence Interval for Model Coefficients: A
level L confidence interval for
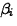 has endpoints
has endpoints
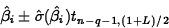
- Confidence Interval for Mean Response: A
level L confidence interval for the mean response at
predictor values
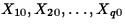 has endpoints
has endpoints
where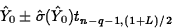
and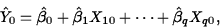
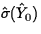 is the estimated standard error of the
response.
is the estimated standard error of the
response.
- Prediction Interval for a Future Observation:
A level L prediction interval for a new response at predictor values
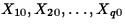 has endpoints
has endpoints
where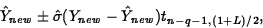
and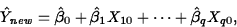
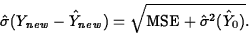
Example:
Here are some intervals for the original fit to the sasdata.cars93a data.
![\begin{figure}
\centerline{\includegraphics*[height=5in,width=5in]{lect8o4.eps}}
\end{figure}](img68.gif)
Multicollinearity is correlation among the predictors.
- Consequences
- o
- Large sampling variability for
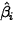
- o
- Questionable interpretation of
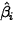 as change in expected response per unit change
in Xi.
as change in expected response per unit change
in Xi.
- Detection
Ri2, the coefficient of multiple determination obtained from regressing Xi on the other Xs, is a measure of how highly correlated Xi is with the other Xs. This leads to two related measures of multicollinearity.- [o] Tolerance TOLi=1-Ri2 Small
TOLi indicates Xi is highly correlated with other Xs. We should begin getting concerned if TOLi<0.1. - [o] VIF VIF stands for variance inflation factor. VIFi=1/TOLi. Large VIFi indicates Xi is highly correlated with other Xs. We should begin getting concerned if VIFi>10.
- Remedial Measures
- o
- Center the Xi (or sometimes the Zi)
- o
- Drop offending Xi
Example:
Here's an example of a model for the sasdata.cars93a data which has lots of multicollinearity:
![\begin{figure}
\centerline{\includegraphics*[height=5in,width=5in]{lect8o5.eps}}
\end{figure}](img70.gif)
Selection of variables in empirical model building is an important task. We consider only one of many possible methods: backward elimination, which consists of starting with all possible Xi in the model and eliminating the non-significant ones one at at time, until we are satisfied with the remaining model.
Example:
Here's an example of empirical model building for the sasdata.cars93a data.