Example
A study was conducted to assess the effects of feedback in a repetitive industrial task. The task was to grind a metal piece to a specified size and shape. Eighteen male workers were divided randomly into three groups. All subjects were given the same introduction to the task.
After beginning the experimental period, the subjects in one group received no feedback about the task, those in the second group were given vague and intermittent feedback, and subjects in the third group were given accurate and continuous feedback. The response consisted of a measure of the value, in dollars, added to production by each subject during the experimental period. This measure was a function of the number of pieces produced, the accuracy of the grinding operation and the amount of reworking necessary in the remaining stages of production. One worker became ill during the study, and his data were dropped. The data, found in SASDATA.FEEDBACK, are:
| Type of Feedback | ||
| None | Vague | Accurate |
| 40.85 | 38.32 | 48.59 |
| 35.21 | 40.26 | 40.71 |
| 38.17 | 47.47 | 45.33 |
| 43.96 | 44.10 | 43.76 |
| 34.88 | 40.09 | 46.41 |
| 42.67 | 44.19 |
![]()
For the present data, i=3, n1=5, and n2=n3=6; ![]() is the
population
mean for the no feedback group, and
is the
population
mean for the no feedback group, and ![]() and
and ![]() are the population
means for the vague and accurate feedback groups, respectively.
are the population
means for the vague and accurate feedback groups, respectively.
The least squares estimator of ![]() is just the mean of the
observations from population i:
is just the mean of the
observations from population i:
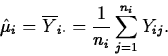
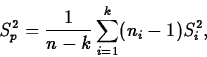
Let's check out the fit of the model to the feedback data.
The residuals
![]()
Here's how to check the fit of the model to the feedback data.
The question researchers most often ask concerning the means model is "Are the population means all equal?"
Formally, the hypotheses are
| H0: | = | = | = | |||||
| Ha: | Not all the population means |
|||||||
| are equal. |
These hypotheses are tested using the F statistic. To see what the F statistic is all about, we first need to learn about partitioning the variation in the response into different components, in what is known as the Analysis of Variance (aka ANOVA).
The total variation in the responses is measured by the total sum of squares, SSTO:
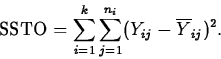
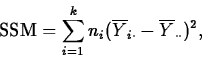
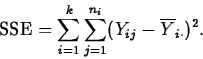
Each SS has associated with it a number, called its degrees of freedom, which counts the number of independent pieces of data going into the SS. The df for SSTO, SSM and SSE are n-1, k-1 and n-k. These df add exactly like their SS.
The mean square is the SS divided by its df. Thus MSM=SSM/(k-1), and MSE=SSE/(n-k).
The test statistic for testing equality of population means is the F statistic F=MSM/MSE. It is compared with its distribution under H0, which is an Fk-1,n-k distribution. Large values of F support Ha over H0.
The information about SS, df, MS and the F test is summarized in an ANOVA table. Let's have a look...
Pairs of population means can be compared using t tests or confidence intervals.
- To test
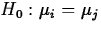 versus
versus 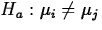 , perform a two-sided t test using the tn-k distribution and the
test statistic
, perform a two-sided t test using the tn-k distribution and the
test statistic
where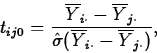
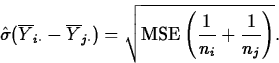
- A level L confidence interval for
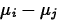 is
is
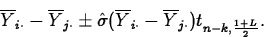
Consider the confidence interval we've just shown for comparing two population means. This type of comparison is called a pairwise comparison, since when we set the confidence level we are only concerned with that particular comparison. If we are doing a lot of these comparisons, we can run into problems interpreting the confidence levels. These problems have to do with
- Formal and informal inference, and the necessity of each.
- Data snooping and its relation to formal and informal inference.
Two multiple comparison procedures which control the overall error rate for all comparisons made are the Bonferroni and Tukey procedures.
- The Tukey procedure considers all pairwise comparisons
and gives an overall level L error rate. It is based on the
distribution of the difference between the largest and
smallest mean of a set of sample means.
When studentized by dividing by estimated standard error, this distribution is called the studentized range distribution. It is suitable for use in data snooping. A level L Tukey interval for
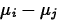 is
is
where qL,k,n-k is the Lth quantile of the studentized range distribution.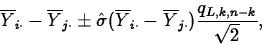
- The Bonferroni is a very general procedure which can be
used for any set of comparisons, not just pairwise
comparisons. However, it can be used for data snooping only
if all comparisons of the type of interest-for example, all
pairwise comparisons-are included among the possible
comparisons. If used for all pairwise comparisons, the
Bonferroni interval for
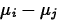 is
is
where N=k(k-1)/2 is the number of pairwise comparisons possible.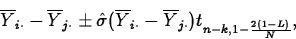
- Nonnormality
- Heteroscedasticity
- Nonindependence
The one-way effects model is the one-way means model parametrized to emphasize the deviations of population means from an overall mean. It is written
![]()
Example
Four types of highway surface are being tested for durability. Engineers obtained 10 different sites on existing highways to test these surfaces. Since the sites are on different types of highways, the engineers decided to divide each site into four equal sections and randomly assign one surface to each section in such a way that all four surface types appear at each site. In reality, the test sites were monitored periodically and a number of measures of wear were taken on each occasion.
The response we will consider is an index of severity of wear, coded on a scale of 0 (no wear) to 100 (severe wear). The data are found in SASDATA.ASPHALT.
Let's look at the data.
One useful model for data of this type is the randomized complete block model:
![]()
Notice that this is an effects model with two factors: blocks,
represented by the ![]() effects and treatments, represented by the
effects and treatments, represented by the
![]() effects. Notice also the model is additive: the
effects add.
effects. Notice also the model is additive: the
effects add.
The least squares estimators of the parameters are:
![]()
The fitted values are
![]()
![]()
![]()
The residuals are, as usual, the observed minus the fitted values,
![]()
The fit is checked by
- Plotting residuals versus predicted, block and treatment.
- Plotting studentized residuals versus t(k-1)(b-1) quantiles.
- Looking at interaction plots.
- Testing for interaction (Tukey).
Let's check out the fit for the asphalt data ourselves.
We test
| = | = | = | = | ||||||
| Not all the population effects
|
|||||||||
| are | 0. |
As for the one-way model, the ANOVA table shows sums of squares, degrees of freedom and mean squares for the RCB model.
Let's look at the analysis for the asphalt data.
- To test
we use the test statistic
H0: 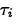
= 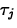
Ha: 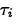
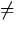
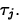
Under H0, tij0 has a t(k-1)(b-1) distribution.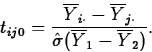
- A level L confidence interval for
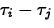 has endpoints
has endpoints
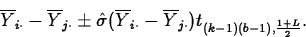
As for the one-way model, we may use either the Bonferroni or the Tukey procedure to compare more than one pair of means.
- A set of Bonferroni confidence intervals for comparing
N pairs of population effects with overall confidence level L,
computes the endpoints of the interval for
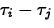 as
as
When doing all k(k-1)/2 pairwise comparisons for k populations, take N=k(k-1)/2.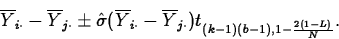
- A set of Tukey confidence intervals for all pairwise
comparisons of k population effects with overall confidence level
L, computes the endpoints of the interval for
 as
as
The confidence level is exact for equal sample sizes from all populations and is conservative if the sample sizes are not all equal.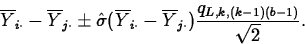
Consider the ANOVA table for the asphalt data considered as a RCBD:
and as a one-way model:
Now consider what this does for estimation. Here is a level 0.95 confidence interval for the difference in mean wear between asphalt types 2 and 3 computed from the one-way model:
(4.915,20.085)
And here is a level 0.95 confidence interval for the difference in mean wear between asphalt types 2 and 3 computed from the RCB model:(8.963,16.037).