This may be much ado about nothing. At the 5% level, there will
be, on average, ![]() significant tests among the
102, even if H0 is true in each case.
significant tests among the
102, even if H0 is true in each case.
- (a)
- (10 points) The scientific hypothesis.
That the new treatment is better than the old.
- (b)
- (10 points) The statistical model.
The two-sample binomial. Here, sample 1 is the 400 individuals assigned to the new treatment, and Y1 is the number of those who required institutionalization, while sample 2 and Y2 are the corresponding quantities for those assigned to the old treatment. We assume
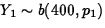 and
and 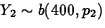 are independent.
are independent.
- (c)
- (10 points) The statistical hypotheses being tested.
H0:p1=p2, Ha:p1<p2
- (d)
- (10 points) The test statistic being used.
The standardized test statistic is
![$Z=(\hat{p}_1-\hat{p}_2)/sqrt{\hat{p}(1-\hat{p})[1/n_1+1/n_2]}$](img4.gif) , where
, where
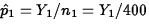 ,
, 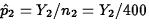 , and
, and
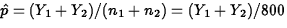 .
.- (e)
- (20 points) The p-value.
Obtain the observed value of the standardized test statistic, z*, by plugging the observed values y1=29 and y2=46 into the above formulas. The result is:
![\begin{displaymath}
z^*=(29/400-46/400)/\sqrt{(75/800)(1-75/800)[1/400+1/400]}=-2.062\end{displaymath}](img8.gif)
The p-value is then
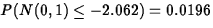 .
.- (f)
- (10 points) The assumptions made, and why they are, or are not, justified.
It is assumed that Y1, n1-Y1, Y2 and n2-Y2 are all at least 10, which is the case here.
- (g)
- (10 points) Your conclusions.
Reject H0 in favor of Ha, at any significance level
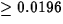 . So at the 0.05 level, reject, at the 0.01 level, do not reject.
. So at the 0.05 level, reject, at the 0.01 level, do not reject.
The observed test statistic is
![]() . We know that
. We know that
![]() , so that
, so that ![]() . Our two
possible choices are p-=0.0274, or p*=0.0274.
. Our two
possible choices are p-=0.0274, or p*=0.0274.
![]() . Solving, we get
. Solving, we get
![]() .
.![]() . Solving, we get
. Solving, we get
![]() .
.