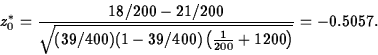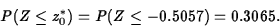Next: About this document ...
Test Your Understanding 5
It has been reported (The Boston Globe, July 31, 1997) that as much as
25% of all worker's compensation claims and 40% of all
payments are attributable to lower back injuries. In an effort
to reduce such injuries, employers have sent workers ``back to
school'' to learn to lift heavy objects safely. Suppose that,
in order to study the effectiveness of such a program, for one
year after the program's completion, you monitor the incidence
of back injury for a random sample of 200 workers who have
taken the program, and a random sample of 200 workers who have
not. Of the 200 workers who completed the course, 18 report at
least one lower back injury during this period and of the
other group, 21 report at least one lower back injury. Is this
convincing evidence for the efficacy of the program? Formulate
the scientific and statistical hypotheses, the statistical
model, and the standardized test statistic. Obtain the
p-value and use it to state your conclusion.
SOLUTION:
- Scientific hypothesis: The program works.
- Statistical model: Two-sample binomial. Let Y1 denote
the number of injuries in the sample of course grads, and
Y2 the number of injuries in the sample of non-grads, and
assume that Y1 and Y2 are independent with
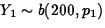 and
and 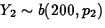 .
. - Statistical hypotheses: H0: p1-p2=0, Ha:
p1-p2<0.
- p-value: First, compute the standardized test
statistic,
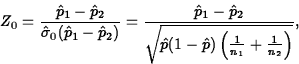
which under H0 has an approximate N(0,1) distribution provided
the sample sizes are large enough. Here, 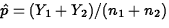 is the pooled estimate of the common value, p, of p1 and p2.
is the pooled estimate of the common value, p, of p1 and p2.
From the data, we have, y1=18, n1-y1=182, y2=21, and
n2-y2=179 are all larger than 10, so the normal approximation is
ok. Also, the pooled estimate of p is
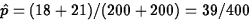 . The observed value of the test
statistic is
. The observed value of the test
statistic is
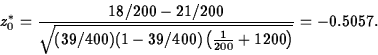
Therefore, the p-value is (Z denotes a N(0,1) random variable)
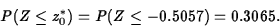
- Conclusion: Do not reject H0. The data supply
insufficient evidence of the efficacy of the program.



Next: About this document ...
Joseph D Petruccelli
11/4/1999
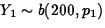 and
and 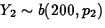 .
.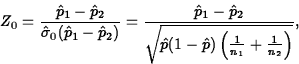
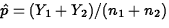 is the pooled estimate of the common value, p, of p1 and p2.
is the pooled estimate of the common value, p, of p1 and p2.
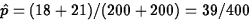 . The observed value of the test
statistic is
. The observed value of the test
statistic is