SOLUTIONS
TEST 1 MA-4451
1. The derivation is similar to the derivation for the transverse vibration problem of the string without the gravitational force. The only difference arises when writing Newton's second law. Here the graviational force has to be added to the equation:
![]()
Thus the problem becomes:

2. a. We extend the function to the symmetric interval [-1,1]. On this interval the function is odd, so we will obtain only a sine expansion:
![]()
The coefficients are:
![]()
b. 0, since the function is continuous at x = 0 and takes the value 0.
c. In order to obtain a cosine Fourier series we consider the even extension of the function on [-1,0]. Thus the extended function will be:
![]()
The Fourier series is:
![]()
where:
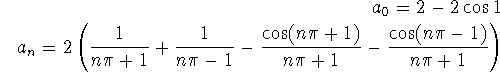
d. The value is 0, since this is the value of the function and the function is continuous.
3. The functions are orthogonal since:
![]()
They are not normalized. Indeed their norms are 2/3 and 8/7.
4. The first equation is elliptic and the second hyperbolic.