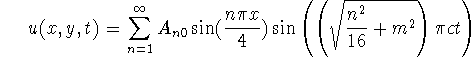TEST 3 MA-4451
SOLUTIONS
1. The Fourier cosine transform will be:
![]()
2.a. Using separation of variables we get:
![]()
and so the two ODEs are:
![]()
For positive eigenvalues we have:
![]()
We remark that C=0 since otherwise Y would be unbounded on the interval y >0. Also, there are no negative or positive eigenvalues (you should check that these would render an unbounded X). From here the solution is of the form:
![]()
From the condition for y=0 we get that:
![]()
and thus A and B are the Fourier cosine and sine transform of the function:
![]()
From page 231 or from the notes the transforms are:
![]()
By substituting in A and B the solution can be explicitly computed.
2.b. By taking the Fourier transform of the PDE with x as variable of integration:
![]()
This is a second order ODE, with solutions of the form:
![]()
Since the solution u has to be bounded for y > 0, it means
that A = 0 for positive ![]() and B = 0 for negative
and B = 0 for negative ![]() . Therefore:
. Therefore:
![]()
or equivalently:
![]()
By transforming the boundary condition we get (see page 231 or notes):
![]()
To determine u we have to compute the inverse transform:
![]()
Remark next that the above integral can be reduced to the solution of 2.a. by substituting in the formula for the complex exponential.
3. Using separation of variables we have:
![]()
Thus:
![]()
From here and the boundary conditions we get the following problems:
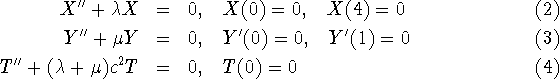
Hence we obtain the following eigenfunctions and eigenvalues:
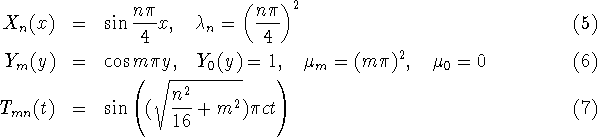
The solution of the PDE can be expressed as a double Fourier sum:
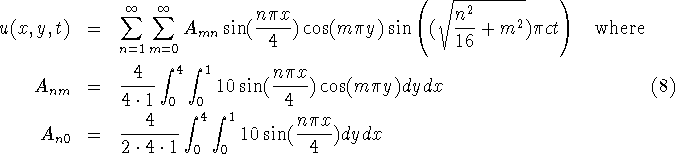
(see table 1 page 248 for the coefficients). The coefficients can be explicitly computed. Remark that the the integral in (8) is zero and thus the solution is of the form: