


MME 524 F' 99 Test 2
- 1.
- (20 points)
A study directed by Dr. Michael Gaziano, a heart specialist at the
Harvard Medical School-affiliated Brigham and Women's Hospital in
Boston, suggests that tea may reduce the chance of a heart attack by
44 percent. Gaziano's study examined 340 men and women who had
suffered heart attacks and matched them by age, sex and neighborhood
with people who had never had a heart attack. It then investigated
their coffee- and tea-drinking habits over the course of a
year. Gaziano thinks that the reason for the reduced incidence of
heart attacks among tea drinkers is that tea contains powerful amounts
of flavonoids, natural substances that make blood cells less prone to
clots, which can cause heart attacks. The study was adjusted for
factors that could have skewed the results, such as smoking, exercise,
alcohol intake and family history of heart trouble. Total calories
consumed, intake of fatty foods and body mass index which compares the
girth of people of different heights to determine obesity was about
the same across the board.
- (a)
- What kind of a study was this? Be as precise as
you can, and justify your answer.
ANS: A retrospective observational study, since subjects
are classified into groups after the fact, and causal factors sought.
(10 points)
- (b)
- Based on this study, is it valid to conclude
that drinking tea causes a reduction in the chance of
a heart attack? Why or why not?
ANS: No, because, even though the researchers tried to
adjust for extraneous factors, this is not a controlled experiment.
(10 points)
- 2.
- (10 points) Figure 1 displays four frequency
histograms, each constructed from a different data set of 200
observations. Each has mean 8.42. Which histogram, that
graphing Y1 (upper left), Y2 (lower left), Y3 (upper right) or
Y4 (lower right), has quartiles Q1=8.09, Q2=9.00,
Q3=9.44? Justify your answer.
Figure 1:
Four frequency histograms for problem 2.
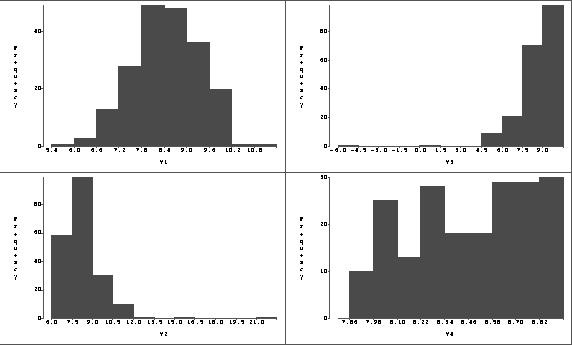 |
ANS: Y3, because of the left skewness.
(10 points)
- 3.
- (30 points) The proper operation of a nuclear
power plant depends on the reactor feedwater system. If the
concentrations of metals, such as iron or copper, are too
high, reactor performance can be adversely affected. In order
to monitor metal concentrations, measurements are taken each
day. A recent set of copper concentration measurements, one
taken on each of 15 successive days, had a mean of 0.2631 ppb
and a standard deviation of 0.0129 ppb. It is desired to
perform statistical inference for the process that produced
these measurements.
- (a)
- If it is desired to estimate the process mean,
what assumptions about the process should be checked?
ANS: Stationarity and normality. (5 points)
- (b)
- Assume you have checked the assumptions in (a),
and there is no evidence that the assumptions do not
hold.
- i.
- Obtain a point estimate for the process
mean copper concentration.
ANS: 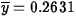 . (5 points)
. (5 points)
- ii.
- Obtain a 95% confidence interval
for the mean. Tell what ``95% confidence'' means here.
ANS: 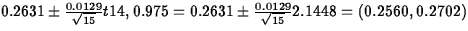 . (10
points) 95% confidence means that in repeated sampling from the same
population, approximately 95% of all intervals constructed in this
way will contain the true population mean. (5 points)
. (10
points) 95% confidence means that in repeated sampling from the same
population, approximately 95% of all intervals constructed in this
way will contain the true population mean. (5 points)
- iii.
- Obtain an interval you are 95%
confident will contain tomorrow's measurement.
ANS: A 95% prediction interval is
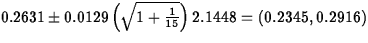 .(5 points)
.(5 points)
- iv.
- Management is interested in an interval
that it can be 95% confident will contain at
least 99% of the population of all possible
measurements. Construct such an interval.
ANS: A 95% tolerance interval for a proportion 0.99 of the
population values is
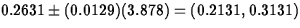 . (5 points)
. (5 points)
- 4.
- (10 points) A survey is to be done to estimate
the proportion of a population with a certain characteristic. How
large a sample is needed to be 99% confident that the estimate will
be within 0.02 of the true proportion?
ANS: n=(0.5)(0.5)(2.5758)2/(0.02)2=4147.
(10 points)
- 5.
- (15 points) The new game ``Textbook Toss'' is
sweeping college campuses. To play the game, the player first
selects a page of his/her textbook at random and then flips a
fair coin. If the coin lands heads, the player wins the number
(in cents) of the selected page (e.g., if page 348 is
selected, the player wins $3.48). If the coin lands tails the
player loses the number of the selected page (e.g., if page
348 is selected, the player loses $3.48).
- (a)
- Suppose the book used in the game has 944 pages,
and let Y denote the amount won by the player on
one play of ``Textbook Toss''. What is the
distribution of Y?
ANS: Y has probability mass function
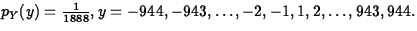 (10 points)
(10 points)
- (b)
- What is the expected value of Y? Support your
answer.
ANS: 0, by the symmetry of the distribution about 0.
(5 points)
- 6.
- (15 points) Historically, a proportion 0.001 of
monthly bills sent to residential customers by a utility company
contains at least one error.
- (a)
- A random sample of 15000 residential bills from
the most recent six-month billing period is taken. If the billing
error rate conforms to the historical proportion, and if presence of
errors in different bills are independent, what kind of distribution
model describes the number of the 15000 bills with errors?
ANS: b(15000,0.001) (5 points)
- (b)
- Of the 15000 bills in the random sample, 25 have
at least one error. Is this convincing evidence that
the proportion of bills with errors has increased from
0.01? Use a large-sample approximation to help you decide.
ANS: Suppose 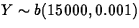 . Then
. Then 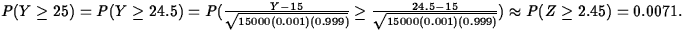 This seems convincing evidence that the proportion of
bills with errors has increased from 0.01. (10 points)
This seems convincing evidence that the proportion of
bills with errors has increased from 0.01. (10 points)
This document was generated using the
LaTeX2HTML translator Version 97.1 (release) (July 13th, 1997)
Copyright © 1993, 1994, 1995, 1996, 1997,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -split 0 test2soln.
The translation was initiated by Joseph D Petruccelli on 1/11/2000



Joseph D Petruccelli
1/11/2000
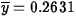 . (5 points)
. (5 points)
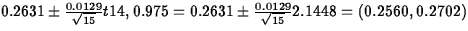 . (10
points) 95% confidence means that in repeated sampling from the same
population, approximately 95% of all intervals constructed in this
way will contain the true population mean. (5 points)
. (10
points) 95% confidence means that in repeated sampling from the same
population, approximately 95% of all intervals constructed in this
way will contain the true population mean. (5 points)
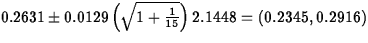 .(5 points)
.(5 points)
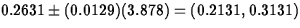 . (5 points)
. (5 points)
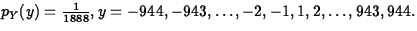 (10 points)
(10 points)
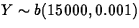 . Then
. Then 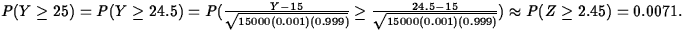 This seems convincing evidence that the proportion of
bills with errors has increased from 0.01. (10 points)
This seems convincing evidence that the proportion of
bills with errors has increased from 0.01. (10 points)
