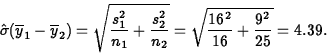CHAPTER 1
INTRODUCTION TO DATA ANALYSIS
- 1.2.
- (10 points) One possibility:

- 1.4.
- (10 points) No data are needed. Ideas about
what affects the phenomenon under study are needed.
- 1.6.
- (10 points) The process is not stationary.
Plot of URATE versus DATE shows this:
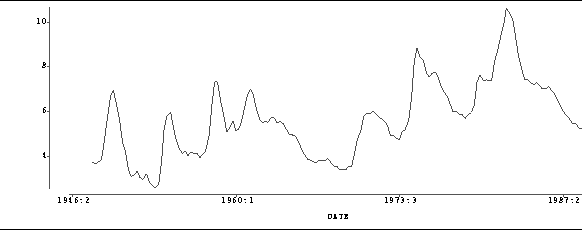
- 1.10.
- (a)
- (4 points)
Stratified plot of percent versus shift:
- (b)
- (6 points: 2 each) Shift 1 has highest and most
consistent percentages.
Shift 2 has second highest and second most
consistent percentages. Shift 3 has lowest and most variable
percentages.
(5 points) Possible causes: Quality of workers
Quality of supervisors
Training
or anything else that makes sense.
- 1.26.
-
- (a)
- (5 points) R&R:repeatability and
reproducibility.
Repeatability measures the consistency of the
scale in repeated measurements of this weight by the same operator.
Reproducibility measures the variation between different operators.
- (b)
- (3 points) Stationarity must be checked.
(2 points) Plot each operator's measurements versus
time.
- (c)
- (5 points) Operator 2 has a much larger
repeatability problem than either operator 1 or
operator 3. Operator 2 should be worked with to
identify and eliminate this problem.
CHAPTER 2
SUMMARIZING DATA
- 2.6.
- (10 points) The bottom fifth cannot pull down a
median. It must be the bottom half or more.
- 2.10.
- 80% (5 points); 0.15 (5 points)
- 2.18.
- (10 points) His quote would imply that the
see-saw could be balanced by putting all the weight on one
side of the fulcrum.
- 2.24.
- Skewed right (5 points), unimodal (5
points). Location: Either the mode at
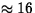 , or the median,
at 17.7. (5 points). Spread: IQR=Q3
-Q1=23.3-12.2=11.1. (5 points)
, or the median,
at 17.7. (5 points). Spread: IQR=Q3
-Q1=23.3-12.2=11.1. (5 points)
- 2.26.
- The data are bimodal (5 points) with modal
bars at 75-85 (mode at 80) (3 points) and 135-145 (mode at 140)
(3 points). Spread of modal regions is 65-105 (3 points)
and 115-165 (3 points) . Possible explanation: Data consist of
two different kinds of concete. (5 points)
CHAPTER 3
DESIGNING STUDIES AND COLLECTING DATA
- 3.2.
- (5 points) The effect of Pepsi over Coke is
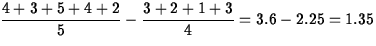
- 3.6.
- Yes it is a controlled experiment since treatments
(old, new: 5 points) are assigned to experimental units
(subjects: 5 points) and a response (removal of clots:
5 points) observed. (Reason it is a controlled
experiment: 10 points)
- 3.14.
- Driver-to-driver variation is included in the
variation between alloys. (5 points) Better to use both
alloys on each car. (5 points)
- 3.20.
- The experimenter could have blocked by kind of
worker and assigned full time workers to both types of
incentive schemes and part time workers to both types of
incentive schemes. (10 points)
- 3.24.
- (a)
- Yes it was a
controlled experiment since treatments (aspirin/placebo) were
assigned to experimental units (mice) and a response
(death/not) observed. (10 points)
- (b)
- Not necessarily. It may be due to the
drug. (10 points)
- 3.32.
- (a)
- This is a sample survey since a
sample is drawn from the target population and the responses observed
from the sample are used to assess the satisfaction of the target
population. (5 points)
- (b)
- This is also a sample survey since a
sample is drawn from the target population and a response measured in
order to summarize responses for the population. (5 points)
- (c)
- This is an observational study, since the
observational units are sampled, and variables are
observed on each. (5 points)
- (d)
- This is a controlled experiment since
treatments (the training program or not) are assigned
to experimental units (workers) and a response
observed (productivity). (5 points)
CHAPTER 4
AN INTRODUCTION TO STATISTICAL MODELING
- 4.14.
- (a)
- (10 points)
| y |
1 |
2 |
3 |
4 |
5 |
6 |
| pY(y) |
1/21 |
2/21 |
3/21 |
4/21 |
5/21 |
6/21 |
- (b)
- E(Y) = (1)(1/21) + (2)(2/21) + (3)(3/21) +
(4)(4/21)+ (5)(5/21) + (6)(6/21) = 13/3 (5 points)
E(Y2) =
(1)(1/21) + (4)(2/21) + (9)(3/21) + (16)(4/21) + (25)(5/21) +
(36)(6/21) = 21
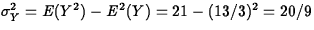 (5 points)
(5 points)
- 4.20.
- (10 points) Let Y = number of weights
ending in 0 or 5. If there is no rounding
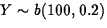 . The observed value of Y is y = 32. Using exact
binomial calculations,
. The observed value of Y is y = 32. Using exact
binomial calculations, 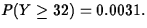
Using the normal approximation,
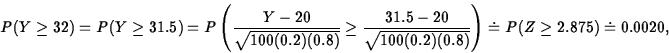
where 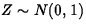 .
.
Either method gives strong evidence against the assumption of
no rounding.
- 4.34.
- (a)
- (10 points)
If Y is the width,
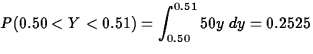 .Of the next 1000, we estimate
.Of the next 1000, we estimate 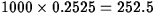 will have widths between 0.50 and 0.51.
will have widths between 0.50 and 0.51.
- (b)
- (10 points) It is
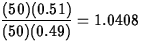 times as likely.
times as likely.
- 4.44.
- (10 points) Let Y = area covered. Want t
such that
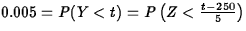 . This means
. This means 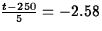 or t = 237.1
or t = 237.1
- 4.50.
- (10 points) Let Y = number of heads. If
fair,
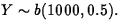 Observed y = 560.
Observed y = 560. 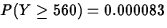 exactly, or using the normal approximation.
exactly, or using the normal approximation.
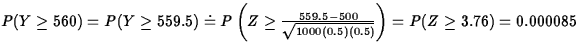 .
.
Either way, this presents strong evidence against the assumption that
the coin is fair.
CHAPTER 5
INTRODUCTION TO INFERENCE:ESTIMATION AND PREDICTION
- 5.6.
- (10 points) Width of
interval:
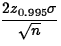 .
.
For
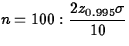 . For
. For 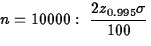 Interval for n = 100 is 10 times as wide (or:difference
is:
Interval for n = 100 is 10 times as wide (or:difference
is: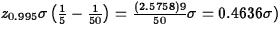
- 5.10.
- Let
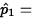 sample proportion of males who
prefer cookie
sample proportion of males who
prefer cookie 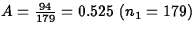
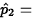 sample proportion of females who prefer cookie
sample proportion of females who prefer cookie
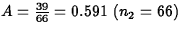
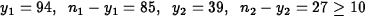 (Assumptions met) (5 points)
(Assumptions met) (5 points)
95% confidence interval for
difference between two population proportions: (5 points)
There is not enough evidence to conclude that the proportion
of females who prefer cookie A is greater than the proportions
of males since 0 is in the interval. (5 points)
- 5.14.
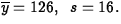
- (a)
- 99% confidence interval for
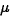 is
is
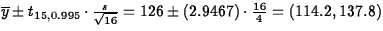 . (5
points) As this interval contains 120, it is not possible to
conclude
. (5
points) As this interval contains 120, it is not possible to
conclude 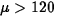 . (5 points)
. (5 points)
- (b)
- 99% prediction interval is
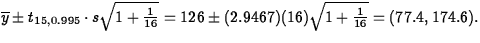 (5 points) We estimate
with 99% confidence that the fire endurance of the next wall tested
will be in the range 77.4 - 174.6. (5 points) 99% confidence
means in repeated samplng, 99% of all 99% prediction intervals so
computed will contain the fire endurance of the next wall. (5
points)
(5 points) We estimate
with 99% confidence that the fire endurance of the next wall tested
will be in the range 77.4 - 174.6. (5 points) 99% confidence
means in repeated samplng, 99% of all 99% prediction intervals so
computed will contain the fire endurance of the next wall. (5
points)
- (c)
- This is a tolerance
interval. (5 points) It is of the form
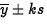 , where k = 3.421. So the
interval is
, where k = 3.421. So the
interval is 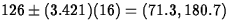 . (5 points)
. (5 points)
- (d)
- The formula
is
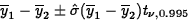 where
where 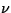 is the
greatest integer less than or equal to
is the
greatest integer less than or equal to
![\begin{displaymath}
\left(\frac{s^2_1}{n_1} + \frac{s^2_2}{n_2}
\right)^2\left/...
...[\frac{(16^2/16)^2}{15} +
\frac{(9^2/25)^2}{24}\right] = 21.
\end{displaymath}](img37.gif)
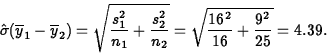
Interval is (5 points)
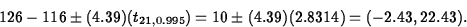
Since the inteval contains , we cannot conclude
there is a difference in mean fire endurance times for
the two types of walls. (5 points)
- 5.30.
- (a)
- Take differences of the Port A and
Port B observations and analyze as paired data. (5 points)
- (b)
- If correlation decreases sufficiently with
distance, use the confidence interval for independent
populations. (5 points)
This document was generated using the
LaTeX2HTML translator Version 97.1 (release) (July 13th, 1997)
Copyright © 1993, 1994, 1995, 1996, 1997,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -split 0 xsols.
The translation was initiated by Joseph D Petruccelli on 12/14/1999



Joseph D Petruccelli
12/14/1999



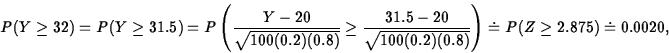
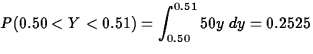 .Of the next 1000, we estimate
.Of the next 1000, we estimate 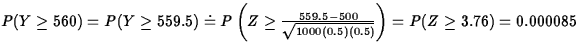 .
.![\begin{displaymath}
\left(\frac{s^2_1}{n_1} + \frac{s^2_2}{n_2}
\right)^2\left/...
...[\frac{(16^2/16)^2}{15} +
\frac{(9^2/25)^2}{24}\right] = 21.
\end{displaymath}](img37.gif)