



Next: Maple at WPI
Up: Getting Started With
Previous: Getting Started With
The software package Maple is an example of a Computer Algebra
System (CAS for short), meaning that it is capable of dealing with
problems in symbolic form. This is in contrast to the numerical
approach that is usually involved in programming computers to solve
problems. A CAS is capable of understanding functions and expressions,
but can also be used to perform algebraic manipulations with
expressions and functions. For example, if you give a CAS an
expression like 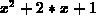 it understands that x is a variable and
Maple can do things like evaluate the expression at a given value of
x, factor the expression, substitute another expression in for x,
multiply two expressions together, and more - all without making
mistakes and much more rapidly than you can do them by hand. Maple
also will let you define your own functions, which can be plotted,
manipulated, combined with other functions, etc. Maple will also
perform many of the manipulations that usually occupy a major part of
a calculus course - differentiation, integration, substitution,
solving differential equations, etc. On the other hand, we will run
into some situations where Maple doesn't do exactly what you would
expect. That is, Maple is not perfect - it has some bugs in it.
Fortunately, there aren't many of these!
it understands that x is a variable and
Maple can do things like evaluate the expression at a given value of
x, factor the expression, substitute another expression in for x,
multiply two expressions together, and more - all without making
mistakes and much more rapidly than you can do them by hand. Maple
also will let you define your own functions, which can be plotted,
manipulated, combined with other functions, etc. Maple will also
perform many of the manipulations that usually occupy a major part of
a calculus course - differentiation, integration, substitution,
solving differential equations, etc. On the other hand, we will run
into some situations where Maple doesn't do exactly what you would
expect. That is, Maple is not perfect - it has some bugs in it.
Fortunately, there aren't many of these!
Maple is a powerful tool that can free you from a lot of calculational
drudgery, but there is a catch. To use it properly, you have to
understand the rules of the game. These rules can be divided into two
parts: rules for Maple syntax, i.e. what are the commands that Maple
understands and how must you express them, and rules of mathematics.
Maple can perform calculations at blinding speed, but you are
responsible for making those calculations meaningful and
mathematically correct. In this section, we will concentrate on the
rules for Maple syntax.




Next: Maple at WPI
Up: Getting Started With
Previous: Getting Started With
William W. Farr
Mon Aug 28 09:31:56 EDT 1995
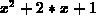 it understands that x is a variable and
Maple can do things like evaluate the expression at a given value of
x, factor the expression, substitute another expression in for x,
multiply two expressions together, and more - all without making
mistakes and much more rapidly than you can do them by hand. Maple
also will let you define your own functions, which can be plotted,
manipulated, combined with other functions, etc. Maple will also
perform many of the manipulations that usually occupy a major part of
a calculus course - differentiation, integration, substitution,
solving differential equations, etc. On the other hand, we will run
into some situations where Maple doesn't do exactly what you would
expect. That is, Maple is not perfect - it has some bugs in it.
Fortunately, there aren't many of these!
it understands that x is a variable and
Maple can do things like evaluate the expression at a given value of
x, factor the expression, substitute another expression in for x,
multiply two expressions together, and more - all without making
mistakes and much more rapidly than you can do them by hand. Maple
also will let you define your own functions, which can be plotted,
manipulated, combined with other functions, etc. Maple will also
perform many of the manipulations that usually occupy a major part of
a calculus course - differentiation, integration, substitution,
solving differential equations, etc. On the other hand, we will run
into some situations where Maple doesn't do exactly what you would
expect. That is, Maple is not perfect - it has some bugs in it.
Fortunately, there aren't many of these!